Основні закони та тотожності алгебри логіки. Поняття про функціонально повні системи, базиси та мінімальні базиси

Логічні функції від двох аргументів.

Ф-ція	x1 x2	Опис
f1(x)					0, константа нуль
F2(x)					х1·x2, x1Ùx2, логічний добуток (кон’юнкція)
F3(x)					х1Dx2, (заборона по х2)
F4(x)					змінна х1
F5(x)					х2Dх1 (заборона по х1)
F6(x)					змінна х2
F7(x)					х1 Å х2 , (сумування по модулю 2)
F8(x)					х1Ú х2 (логічна сума, диз’юнкція)
F9(x)					х1¯х2 (функція Пірса)
F10(x)					х1=х2, (логічна рівнозначність)
F11(x)					2 інверсія х2
F12(x)					х2®х1, імплікація від х2 до х1
F13(x)					1, інверсія х1
F14(x)					х1®х2, (імплікація від х1 до х2)
F15(x)					х1| х2, (функція Шеффера)
F16(x)					1, константа одиниця

1) 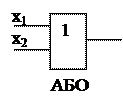f₈ = х₁Ú х₂ (логічна сума, диз’юнкція) операція АБО (OR)

2) 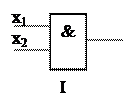f₂ = х₁·x₂, x₁Ùx₂, логічний добуток (кон’юнкція)

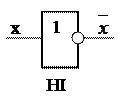операція І (AND).

3) f₁₁ = ₂ інверсія х₂ НІ (NOT).

За допомогою цих 3 операцій можна здійснити всі операції.

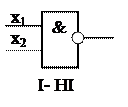
4) 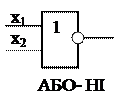f₉ = 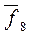функція Даггера, операція АБО-НІ

5) f₁₅ = 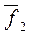= 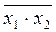функція Шеффера І - НІ

Приклади:

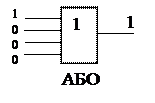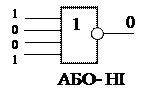Основні закони алгебри логіки:

1. асоціативний (сполучний) закон: (х1·х2)·х₃ = х₁·(х2·х3);

(х₁+х₂)+х₃=х₁+(х₂+х₃)=х₁+х₂+х₃.

2. дистрибутивний (розподільчий) закон: (х₁+х₂)х₃ = х1·х3+х2·х3;

3. комутативний (переставний) закон: х_{1 ·}х₂ = х₂ ·х₁; х₁+х₂=х₂+х₁.

Основні співвідношення для інверсії:

1.

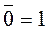
2.

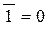
3. Закон подвійного заперечення: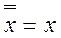

Основні тотожності для диз’юнкції і кон’юнкції.

диз’юнкція кон’юнкція

0+х = х х·0 = 0

х+1 = 1 х·1 = х

х+х = х х·х = х

х+= 1 х·= 0

х+х+...+х=х х·х·...·х=х

Перетворення де Моргана (застосовується дія переходу від диз’юнкції до кон’юнкції і навпаки)

Базис – це набір булевих функцій, виключення з якого любої функції перетворює систему булевих функцій в неповну.

Приклади базисів: 1) І, АБО, НІ; 2)"І – НІ"; 3) "АБО – НІ".

Приклади:

І. f = х₁Úх₂·₃·х₄Úх₅Ú₁Úх₂·(₃·х₄Úх₂·₃) =1

ІІ. f = х₂·х₃·(х₁Úх₂·х₃·₄)·(₃Ú₃)Úх₂ = 0Úх₂ = х₂

ІІІ. Перетворити в базисі І-НІ функцію

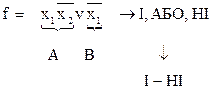
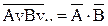
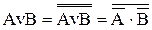
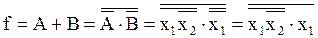
IV. f = x₁Ú₂·(₃Úx₂·x₁) ® І – АБО – НІ ® І – НІ

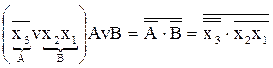
V. f = 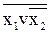Úx₂.₃) ® І – АБО – НІ® І – НІ

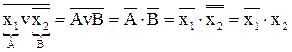
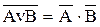
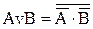
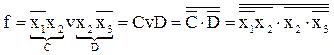
VI. Перетворити функцію в базисі АБО – НІ

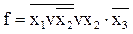І, АБО, НІ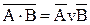

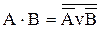
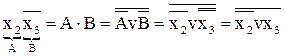
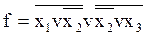
VII. 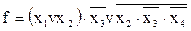І, АБО, НІ ® АБО – НІ

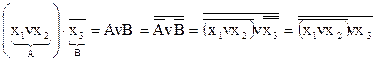
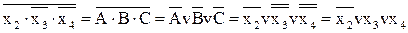
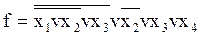
Приклад 1.

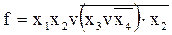® І, АБО, НЕ ® І – НЕ

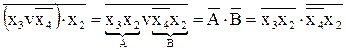
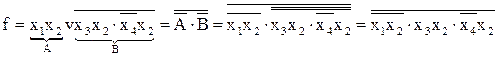
Приклад 2.

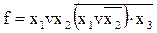® І, АБО, НІ ® АБО – НІ

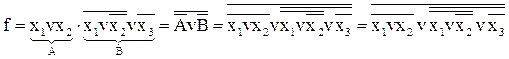
Дата добавления: 2014-10-15