Плоские электромагнитные волны в среде без потерь, и в среде с потерями

Монохроматическую электромагнитную волну, волновые поверхности которой представляют собой параллельные плоскости, называют плоской волной. Плоскую волну, во всех точках каждой волновой поверхности которо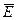й и 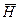имеют одно и тоже значение и направление, называют однородной плоской волной.

Для ПВ сделаем предложение: комплексный вектор Пойнтинга ориентирован вдоль оси z и, следовательно, имеет только одну составляющую П_z откуда следует, что E_z и H_z=0.

При этом, т. к. волна однородна, т. е. амплитуды вдоль волнового фронта неизменны (не зависят от x и y), то в волновом уравнении .

В общем случае 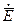будет иметь и 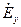однако можно предположить, что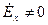 . В этом случае волна называется линейно поляризованной, а xoz-плоскостью поляризации. Естественно будет находится в плоскости yoz.

x

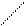Е

z

y Н

Магнитный вектор может быть найден из второго уравнения.

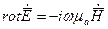
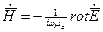
Т. к. , 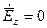получим: ;

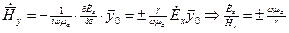. Т. к. Вектор имеет только одну составляющую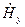

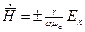при этом между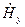 существует связь.

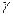-коэффициент распространения. Если 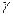-вещественно, т. е. среда без потерь, то и 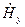колеблются в фазе, т. е. ЭМВ переносит в среде без потерь только активную мощность.

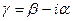
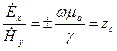, где - постоянная характеристического (волнового) сопротивления среди распространения. Для вакуума среди без потерь

тогда зная можно в ПВ по одному из векторов находить другой. Найдем фазовую скорость: в вакууме

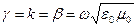
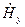Запишем общее соотношение между и плоской волны.

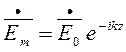
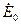и 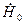, в точке z=0.

Для вещественных частот ,

При наличии потерь необходимо параметр к считать комплексной величиной:

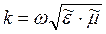
Пусть , 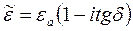где

Тогда, считая

находим выражение для

Т.о., после плоской волны в среде с проводимостью

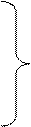
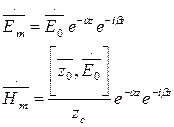
Наличие потерь приводит к уменьшению ½Z _c½, т.е. к увеличению 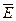и 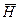. Если 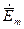имеет лишь одну составляющую 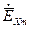, то 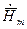тоже будет иметь одну составляющую 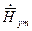. Для мгновенных значений получим:

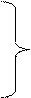Вставить формулу

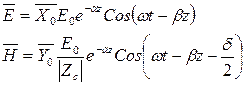
Из полученных формул вытекает, что поле плоской волны обладает следующими свойствам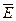и: и 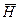перпендикулярны друг другу и направлению распространения волны (оси Z), т.е., волна является поперечной. Поверхности равных фаз определяются уравнением Z= const и представляют собой плоскости, перпендикулярные оси Z. Амплитуды векторов 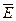и 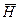экспоненциально убывают вдоль оси Z, что определяется множителем e^-aZ. Постоянную a называют коэффициентом затухания. Между векторам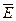и и 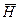имеется фазовый сдвиг .

Фазовая скорость плоской волны

т.к. 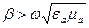то V_ф меньше фазовой скорости в среде без потерь с теми же значениями параметров e_a и m_а. В рассматриваемом случае V_ф зависит от частоты. С увеличением последней она возрастает.

Длина волны меньше длины волны в среде без потерь с теми же e_a и m_а. Волновое сопротивление среды с отличной от «0» проводимостью - комплексная величина, зависящая от частоты.

Основное отличие состоит в том, что в среде без потерь параметры плоской волны одинаковы при любых частотах, а в среде с проводимостью зависят от частоты. Зависимость свойств волны от частоты называется дисперсией.

Дата добавления: 2014-10-15