Уравнения Максвелла с учетом сторонних источников. Электрический баланс электромагнитного поля

Энергия ЭМП является важной характеристикой. Максвелл показал, что полная энергия ЭМП, заключенная внутри объема V складывается из энергии электрического W_Э и магнитного W_М полей.

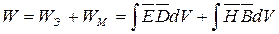
Используя материальные уравнения и переходя к действующим значениям векторов, получим:

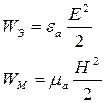
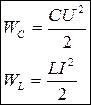
Энергия поля может меняться вследствие следующих фактов:

1. Превращения в другие виды.

2. Обмен энергии между рассматриваемым объектом и окружающим пространством.

3. Работой так называемых сторонних источников, которые могут либо увеличивать, либо уменьшать запас энергии в объеме.

Под сторонними источниками понимают токи, создаваемые внешними источниками, независимыми от возбуждаемого электромагнитного поля. Примером сторонних токов могут быть токи в антеннах, которые создают ЭМП во внешнем пространстве. Плотность сторонних токов принято обозначать .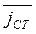

С учетом сторонних токов первое уравнение Максвелла запишется в виде:

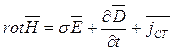
Интенсивность излучения характеризуется векторной величенной, набиваемой вектором Пойнитинга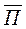

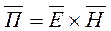
Величена 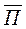равна отношению энергии проходящей за время Dt через площадку DS, расположенную перпендикулярно направлению распространения.

Изменение энергии ЭМП внутри объема V ограниченного поверхностью S:

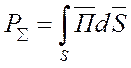
если знак интеграла отрицателен, то поток энергии направлен внутрь, а если положителен, то из него.

Используя теорему Остроградского – Гауса:

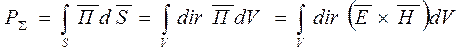
Воспользовавшись тождеством векторного анализа:

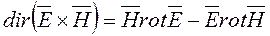, получаем:

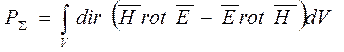, если учесть выражения для из уравнений Максвелла, то

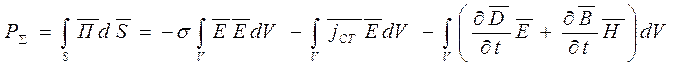
Первый интеграл в правой части – мгновенная мощность потерь внутри объема V, обусловленная наличием тока проводимости.

Второе слагаемое определяет мгновенную мощность сторонних источников, которая может либо втекать в данный объем, либо вытекать из него.

Третье слагаемое можно представить в виде:

, тогда ,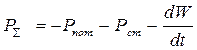

где 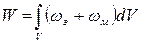энергия ЭМП внутри объема V.

Эта теорема является выражением баланса энергии электромагнитного поля внутри некоторого объема V или закона сохранения энергии. Т.е. изменение энергии поля в некотором объеме происходит из-за потерь, наличия сторонних источников и излучения.

Монохроматическое электромагнитное поле. Классификация электромагнитных явлений.

Для удобства решений поля условно разделяют на статические, стационарные и квази стационарные.

Решение уравнений Максвелла представляет собой сложную математическую задачу. Упростить задачу решения можно для монохроматических электромагнитных полей, т. е. для полей, изменяющихся во времени по гармоническому закону с частотой 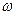. Это упрощение возможно путём использования так называемого метода комплексных амплитуд. В этом случае вместо любой скалярной функции 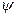, изменяются по закону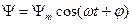; 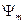-амплитуда, 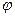-начальная фаза, -круговая частота, вводится в рассмотрение комплексная функция 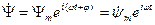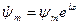- комплексная амплитуда функции 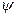. 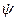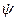Для перехода от к исходной нужно взять от реальную часть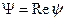

Аналогично вместо вектора

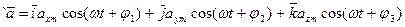можно ввести комплексный вектор

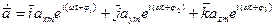
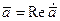
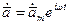
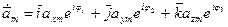-комплексная амплитуда .

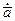Определение комплексных функций во многих случаях проще, чем исходных. Это объясняется тем, что дифференцирование комплексной функции по времени равносильно умножению ее на 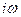: 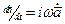, а интегрирование по времени--делению на :

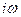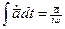
При изучении монохроматических электромагнитных полей вместо векторов 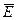и 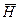можно рассматривать комплексные векторы 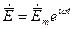и 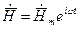, связанные с векторам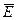ии 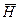соотношениями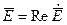 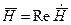. Если

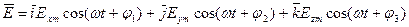то

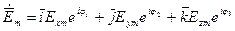--комплексная амплитуда.

Перейдём в системе уравнений Максвелла к комплексным векторам 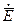и .

Первое уравнение: 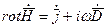т. к. ,

.

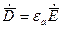
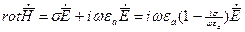Введя обозначение: перепишем уравнение в форме:

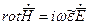-первое уравнение Максвелла для монохроматического поля.

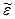-комплексная диэлектрическая проницаемость среды. Кроме того это же уравнение может быть записано в виде: .

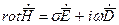Аналогично второе уравнение Максвелла можно записать в форме: 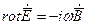, а также:; ; ; .

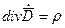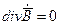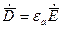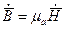Составим уравнение баланса для средних за период значений мощности монохроматического ЭМП.

Величина вектора Пойнтинга показывает плотность потока мощности т. е. мощность, проходящую через площадку размером 1м², расположенную перпендикулярно направлению распространению энергии.

Рассмотрим выражение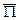через комплексные амплитуды гармонических полей 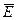и .

.

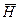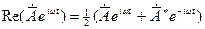
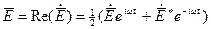
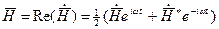Представив эти выражения для вектора Пойнтинга

.

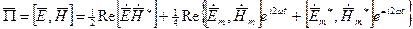Первое слагаемое в правой части формулы не зависит от времени. Остальные слагаемые изменяются с двойной частотой и поэтому их среднее за период значение равно нулю. Следовательно, при усреднении вектора Пойнтинга, получаем:

.

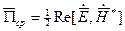Комплексный вектор 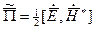называют комплексным вектором Пойнтинга.

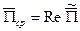. Средний поток энергии через поверхность S, ограничивающую рассматриваемый объем V: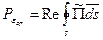

.

Аналогично вычисляются средние значения остальных величин, входящих в уравнение баланса.

Дж. потери .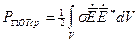

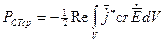Среднее значение электрической и магнитной энергии

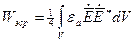
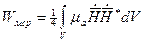
а среднее за период изменение электромагнитной энергии = 0. 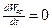, таким образом подходим к уравнению: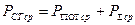

Классификация электромагнитных явлений.

Можно выделить несколько видов полей:

1. Электростатическое поле.

Описывается системой дифференциальных уравнений Максвелла в предложении, что векторы поля не зависят от времени и отсутствует перемещение зарядов.

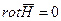
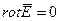
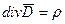
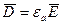
Из уравнений следует, что оно является потенциальным, а его силовые линии начинаются и заканчиваются на зарядах. Вектор 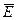можно представить в виде градиента скалярной функции и, называемой электростатическим потенциалом.

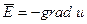
Энергия электростатического поля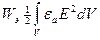

Явления, описываемые вышеприведёнными уравнениями- электростатические.

Стационарное электромагнитное поле.

Это неизменное во времени ЭМП, существующее при наличии постоянного тока.

; ; ; ; ; .

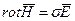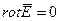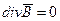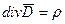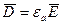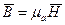Стационарные электромагнитные явления.

Магнитостатические явления характеризуются уравнениями: 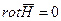; ; 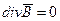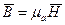. И представляют поля, создаваемые постоянными магнитами.

В качестве самостоятельного класса выделяют квази стационарные процессы, т. е. процессы, протекающие достаточно медленно.

В этом случае в первом уравнении при наличии тока проводимости можно пренебречь током смещения. .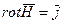

В остальных случаях используют полную систему уравнений Максвелла.

Дата добавления: 2014-10-15