Граничные условия для векторов электрического поля

Граничные условия. Волновые уравнения.

Уравнения Максвелла в дифференциальной форме справедливы для сред, параметры которых не испытывают скачков в зависимости от координат. На практике встречаются случаи, когда рассматриваемая область состоит из разных сред. В этом случае надо исходить из уравнений Максвелла в интегральной форме.

Соотношения, показывающие связь между значениями векторов ЭМП в различных средах у поверхности раздела называются граничными условиями.

Условия для нормальных составляющих векторов 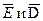. Построим на D S прямой цилиндр высотой D h. Применим третье уравнение в интегральной форме:

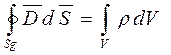
где S_g – поверхность, а V – объем цилиндра.

S_g = D S₁+D S_бок+D S₂ отсюда вытекает:

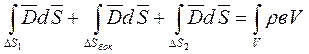устремляем D h к 0.

В пределе D S₁=D S=D S₂, 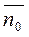- нормаль к поверхности.

При существовании поверхностного заряда.

Граничные условия показывают, что при переходе через поверхность раздела, несущую поверхностный заряд нормальной составляющей вектора 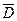претерпевает скачкообразные изменения. Причем величина скачка равна r_S. Если r_S=0, то D_1n=D_2n.

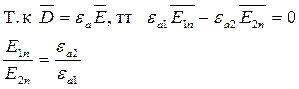
Дата добавления: 2014-10-15