Модели многофакторного прогнозирования

Прогнозирование по одномерному временному ряду, рассмотренное выше, не учитывает взаимодействие изучаемого процесса с другими экономическими явлениями, имеющими место в реальной действительности. Для учета причин, определяющих динамику развития процесса, перейдем к моделям многофакторного прогнозирования.

В построении таких моделей по временным рядам есть ряд особенностей. Если временные ряды содержат сезонные или циклические колебания, то перед проведением дальнейшего исследования взаимосвязи необходимо устранить сезонную или циклическую компоненту. Наличие данных компонент приводит к завышению истинных показателей силы и тесноты связи, если оба ряда содержат колебания одинаковой периодичности, либо к занижению этих показателей, если периодичность содержится только в одном ряду или если период колебаний различен.

Построение многофакторных моделей произведем на данных с квартальной периодичностью.

Так как исследуемые временные ряды содержат сезонную компоненту, то для их моделирования выберем регрессионную модель с сезонными фиктивными переменными, являющуюся аналогом аддитивной модели временного ряда. Сезонные фиктивные переменные будут дополнительно оценивать вклад причин, действующих на интервале наблюдения. Временная ограниченность базы данных вынуждает ограничиться количеством факторов, включаемых в модель регрессии, поэтому включим только один фактор.

Оцениваемая модель имеет следующий вид:

,

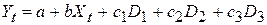где 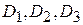- фиктивные переменные;

- их коэффициенты, отражают численную величину эффекта, вызванного сменой года. Количество фиктивных переменных в данной модели должно быть на единицу меньше числа моментов времени внутри одного цикла колебаний. Каждая фиктивная переменная отражает сезонную компоненту временного ряда для одного какого-то периода, в данном случае квартале. Она равна единице для данного периода и нулю для всех остальных периодов, например:

.

В набор факторов-кандидатов, оказывающих влияние на объем предоставляемых кредитов банком (Y), включим следующие:

1. Процентные ставки по кредитам(X1) (источник ЦБР);

2. Процентные ставки по межбанковским кредитам (X2) (источник ЦБР);

3. Помесячный объем выпуска продукции (X3) – источник: Госкомстат;

4. Объем привлеченных средств банком (X4).

Наибольшее влияние на объем предоставляемых кредитов оказывает объем привлеченных средств банков (таб. 9.10).

Таблица 9.10

Матрица парных корреляций

Переменная	Y	X1	X2	X3	X4
Y
X1	-0,875
X2	-0,687	0,665
X3	0,889	-0,927	-0,773
X4	0,962	-0,832	-0,642	0,898

Включение фактора времени позволило значительно улучшить модель. После оценки параметров модель примет вид (табл. 9.11).

Таблица 9.11

Оценка параметров регрессии для временного ряда «Кредиты»

Номер фактора	Коэффициент Регрессии	Стандартная ошибка коэффициента	T – значение
Св. член	42434,473	6124,604	6,929
Х4	0,366	5790,417	-1,426
D1	-8258,518	6146,917	-0,352
D2	-2161,553	6102,35	-1,560
D3	-9520,45	0,189	1,937
Т	5667,306	1208,672	4,689
Критерий Дарбина-Уотсона	1,624
Критерий серий	Kmax =4 V =7
RS – критерий	3,361
Множественный коэффициент корреляции	0,996
F-значение	618,711
Средний модуль ошибки	6,174%

Параметр а =42434,473 есть сумма начального уровня и сезонной компоненты в третьем квартале. Сезонные колебания в остальных кварталах приводят к снижению этой величины, о чем свидетельствуют отрицательные оценки параметров.

Параметры фиктивных переменных не равны значениям сезонной компонент, так как они характеризуют не сезонные изменения уровней ряда, а их отклонения от уровня в третьем квартале. Влияние сезонной компоненты не значимо в первом квартале, так как незначительно отклоняется по сравнению с третьим кварталом. Фактическое значение F-критерия равное 618,711 при 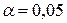превышает табличное (3,33), т.е. уравнение признается статистически значимым.

Независимость ряда остатков подтверждается сравнением r₁ =0,128 с критическим значением при уровне значимости 0,05, модель является адекватной (рис.9.17).

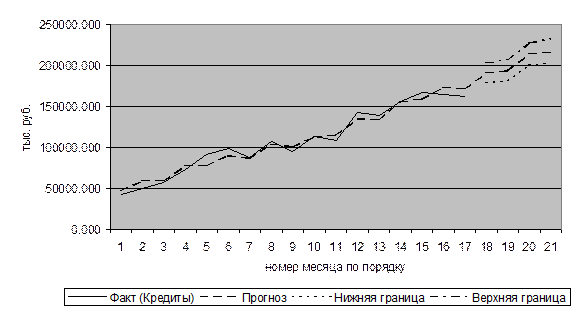Рис. 9.17. Модель регрессии с фиктивными сезонными коэффициентами

для временного ряда «Кредиты»

Для построения модели регрессии для показателя «Выпущенные банком ценные бумаги» в качестве факторов рассмотрим (таб. 9.12):

1. Индекс РТС (Х1) – источник: ЦБР, РТС;

2. Индексы промышленности (Х2) – источник: Госкомстат;

Таблица 9.12

Матрица парных корреляций

Переменная	Y	X1	X2
Y
X1	0,596
X2	0,781	0,710

Наибольшее влияние на выпуск ценных бумаг банком оказывает индекс промышленности. Для моделирования временного ряда применим фиктивные сезонные переменные. Большинство оценок коэффициентов регрессии выпуска ценных бумаг от индекса промышленности и фиктивных переменных оказались незначимыми. Построим регрессию от индекса РТС, включение фактора времени позволило значительно улучшить модель. После оценки уравнение регрессии примет вид (табл. 9.13):

Таблица 9.13.

Оценка параметров регрессии для временного ряда «Выпущенные

банком ценные бумаги»

Номер фактора	Коэффициент Регрессии	Стандартная ошибка коэффициента	T – значение
Св. член	10643,112	1818,704	5,852
Х1	-34,359	16,595	-2,07
D1	-939,029	1957,072	-0,48
D2	6301,061	1971,922	3,195
D3	-157,859	1857,772	-0,085
Т	2038,622	330,747	6,164
Критерий Дарбина-Уотсона	2,058
Критерий серий	Kmax =5 V =9
RS – критерий	3,745
Множественный коэффициент корреляции	0,992
F-значение	278,136
Средний модуль ошибки	8,4%

Независимость ряда остатков подтверждается сравнением r₁ =0,064 с критическим значением при уровне значимости 0,05, модель является адекватной (рис. 9.18).

Фактическое значение F-критерия равное 278,136 при 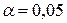превышает табличное (3,33), т.е. уравнение признается статистически значимым. Параметр а =10643,112 есть сумма начального уровня и сезонной компоненты в первом квартале. Сезонные колебания во втором и четвертом квартале приводят к снижению этой величины, о чем свидетельствуют отрицательные оценки параметров. В третьем квартале наблюдаем увеличение объема выпуска банком ценных бумаг по сравнению с первым кварталом.

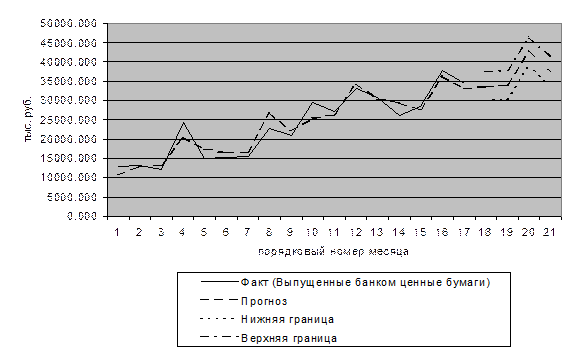Рис. 9.18. Модель регрессии с фиктивными сезонными переменными для

временного ряда «Выпущенные банком ценные бумаги»

Для получения прогнозных значений зависимых переменных подставим в уравнение ожидаемые значения факторов, полученные экстраполяцией.

В таблице 9.14 приведены результаты точечного и интервального (с вероятностью 70%) прогноза показателей по построенным моделям. Доверительные интервалы в многофакторных моделях зависят от стандартной ошибки, удаления прогнозного значения факторов от своего среднего значения, количества наблюдений и уровня значимости прогноза. Введение в модель фиктивных переменных способно отразить влияние сезонных изменений уровней, чем больше сезонный эффект, тем шире величина доверительного интервала.

Таблица 9.14

Моделируемый ряд	Упреждение	Прогноз	Нижняя граница	Верхняя граница
Кредиты		190983,859 194133,953 214400,609 217185,531	175555,504 177975,948 197159,744 198446,957	206412,215 210251,958 231,641,474 235924,105
Ценные бумаги		33594,82 34007,238 42596,773 37628,738	28924,035 29394,76 37980,995 32772,741	38265,606 38619,717 47216,552 42484,736

Интервальные прогнозы дают ценную информацию о развитии изучаемых систем, и полезны как для краткосрочного, так и анализа долгосрочных тенденций.

При построении многофакторных моделей существенно расширяется набор необходимых для этого данных, что не всегда осуществимо. Поэтому на практике прогнозирование по одномерному временному ряду часто оказывается единственно приемлемым способом расчета прогнозных вариантов с позиций информационной обеспеченности и требуемой надежности.

Контрольные вопросы и задания

1. Перечислите основные шаги алгоритма моделирования тренд-сезонного экономического процесса.

2. В таблице приведены данные по выручке от реализации лако-красочной продукции, млн. руб.

Месяц	1 год	2 год	3 год
I квартал	22 095.00	26 581.00	24 880.00
II квартал	26 541.00	26 197.00	37 077.00
III квартал	37 347.00	40 389.00	57 016.00
IV квартал	37 590.00	38 086.00	44 843.00

а) Построить модель регрессии с включением фактора времени и фиктивных переменных.

б) Построить точечный прогноз на четыре шага вперед.

в) Построить интервальный прогноз на тот же период при достоверности прогноза 85%.

г) Результаты прогнозирования изобразить на графике.

3. По данным задания 2:

а) Построить аддитивную модель Хольта-Уинтерса с параметрами сглаживания 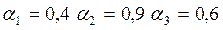и мультипликативную модель Холта-Уинтерса с параметрами сглаживания .

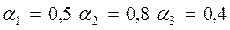б) Оценить качество построенных моделей и выбрать лучшую.

в) По лучшей модели построить точечный прогноз на четыре шага вперед.

г) Построить интервальный прогноз на тот же период при достоверности прогноза 75%.

д) Результаты прогнозирования изобразить на графике.

Литература

1. Айвазян С.А. Енюков И.С., Мешалкин Л.Д. Прикладная статистика: Основы моделирования и первичная обработка данных. Справочное издание под ред. Айвазяна С.А. – М.: Финансы и статистика, 1983. – 471 с.

2. Андерсон Т. Введение в многомерный статистический анализ. -М.: Физматгиз, 1963. - 500 с.

3. Андерсон Т. Статистический анализ временных рядов. -М.: Мир, 1976. - 755 с.

4. Арсеньев Ю.Н., Шелобаев С.И. Методы и модели оптимизации ресурсов субъектов рынка: Учебное пособие. М.: Высшая школа, 1998

5. Арсеньев Ю.Н., Шелобаев С.И. Принятие решений. Интегрированные интеллектуальные системы: Учебное пособие для вузов. М.: ЮНИТИ-ДАНА, 2003

6. Арсеньев Ю.Н., Шелобаев С.И., Давыдова Т.Ю. Управление персоналом. Модели управления: Учебное пособие для вузов. М.: ЮНИТИ-ДАНА, 2005

7. Арсеньев Ю.Н., Шелобаев С.И., Давыдова Т.Ю. Информационные системы и технологии. Экономика. Управление. Бизнес.: Учебное пособие для вузов. М.: ЮНИТИ-ДАНА, 2006

8. Арсеньев Ю.Н., Шелобаев С.И. Оптимизация банковских процессов и принятия решений. – М.: Высшая школа, 1999. – 608 с.

9. Афанасьев В.Н., Юзбашев М.М. Анализ временных рядов и прогнозирование.- М.: Финансы и статистика, 2001. – 228 с.

10. Балдин К.В., Быстров О.Ф., Соколов М.М. Эконометрика: Учеб. пособие для вузов. – 2-е изд., перераб. и доп. – М.:ЮНИТИ-ДАНА, 2004. – 254 с.

11. Баласанов Ю.Г. Дойников А.Н. Королев М.Ф., Юровский А.Ю. Прикладной анализ временных рядов с программой ЭВРИСТА. Центр СП «Диалог» МГУ, 1991. – 328 с.

12. Бендат Дж., Пирсол А. Прикладной анализ случайных данных. – М.: Мир, 1989. – 540 с.

13. Бендат Дж., Пирсол А. Применение корреляционного и спектрального анализа. – М.: Мир, 1979. – 311 с.

14. Бигель Дж. Управление производством. Количественный подход. – М.: Мир, 1993. – 305 с.

15. Бокс Дж., Дженкинс Г. Анализ временных рядов. Прогноз и управление. Пер. с англ. - М.: Мир, вып.1, 1974. - 197 с.

16. Бриллинджер Д. Временные ряды. Обработка данных и теория. - М.: Мир, 1980. -536 с.

17. Вайну Я.Я. - Ф. Корреляция рядов динамики. - М.: Статистика, 1977. - 118 с.

18. Гинсбург А.М. Сезонность и сезонные колебания. – М.: Гостехиздат, 1929. – 39 с.

19. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2000. – 479 с.

20. Гольдштейн А.И. Теоретическая разработка вопросов исчисления сезонных изменений и новый метод их исчисления. - В кн.: Труды конъюнктурного института. -М.: Изд. ЦСУ СССР, 1929.- с. 19-33.

21. Горчаков А.Л., Орлова Н.В. Компьютерные экономико-математические модели. М.: ЮНИТИ, 1995. – 136 с.

22. Гренджер К., Хатанака М. Спектральный анализ временных рядов в экономике. Пер. с англ. - М.: Статистика, 1972. - 311 с.

23. Дженкинс Г., Ваттс Д. Спектральный анализ и его приложения. Пер. с англ. - М.: Мир, вып I, 1971. - 316 c.

24. Дженкинс Г., Ваттс Д. Спектральный анализ и его приложения. Пер. с англ. - М.: Мир, вып.2, 1971. - 455 с.

25. Джонстон Дж. Эконометрические методы. – М.: Статистика, 1980. – 444 с.

26. Доугерти К. Введение в эконометрику. – М.: ИНФРА-М, 1997. – 402 с.

27. Евсюков В.В., Трошин С.В., Шибаев Л.Л. Шелобаева И.С. Информационная безопасность в банковском деле. Тула, изд. Центр ТГПУ им. Л.Н. Толстого, 2001.- 186 с.

28. Кендэлл М., Стьюарт А. Многомерный статистический анализ и временные ряды. Пер. с англ. - М.: Наука, 1976. - 736 с.

29. Кильдишев Г.С., Френкель А.А. Анализ временных рядов и прогнозирование. - М.: Статистика, 1973. - 103 с.

30. Кобелев Н.Б. Практика применения экономико-математических методов и моделей. – М.: Финстатинформ, 2000. – 246 с.

31. Кобринский Н.Е., Кузьмин В.И. Точность экономико-математических моделей. - М.: Финансы и статистика, 1981. -254 с.

32. Крамер Г. Математические методы статистики. Пер. с англ.- М.: Мир, 1975. - 648 с.

33. Кузьмин В.И., Половников В.А., Новиков А.И. Методы научно-технического прогнозирования. - М.: МЭСИ, 1980. - 126 с.

34. Кулаичев А.П. Методы и средства анализа данных в среде Windows. – М.: Информатика и компьютеры, 1998. – 270 с.

35. Кутуков В.Б. Основы финансовой и страховой математики. М.: Дело, 1998. – 304 с.

36. Левицкий Е.М. Адаптивные экономические модели. - Новосибирск: Наука, 1981.- 222 с.

37. Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования. - М.: Статистика, 1979. - 253 с.

38. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс: Учеб. – 6-е изд., перер. и доп. – М.: Дело, 2004. – 576 с.

39. Орехов Н.А., Лёвин А.Г., Горбунов Е.А. Математические методы и модели в экономике: Учебное пособие для вузов/ под ред. Проф. Н.А. Орехова. – М.: ЮНИТИ-ДАНА, 2004. – 302 с.

40. Орлова И.В. Экономико-математические методы и модели. Выполнение расчетов в среде Excel. – М.: Финстатинформ, 2000. – 136 с.

41. Орлова И.В., Половников В.А. Экономико-математические методы и модели: Учеб. пособие. – М.: Вузовский учебник, 2007. – 365 с.

42. Половников В.А. Анализ и прогнозирование транспортной работы морского флота. – М.: Транспорт, 1983. – 224 с.

43. Половников В.А., Горчаков А.А. Модели и методы экономического прогнозирования. - М.: МЭСИ, 1980. -116 с.

44. Половников В.А., Скучалина Л.М. Методы и модели экономического прогнозирования. - М.: МЭСИ, 1981. -78 с.

45. Справочник по прикладной статистике. В 2-х т. Т. 1: Пер. с англ. /Под ред Э. Ллойда, У. Ледермана, Ю.Н. Тюрина. – М.: Финансы и статистика, 1989. - 510 с.

46. Справочник по прикладной статистике. В 2-х т. Т. 2: Пер. с англ. /Под ред Э. Ллойда, У. Ледермана, С.А. Айвазяна, Ю.Н. Тюрина. – М.: Финансы и статистика, 1990. - 526 с.

47. СтатЭксперт. Программа статистического анализа и прогнозирования СтатЭксперт: Руководство пользователя – М.: Росэкспертиза, 1996. – 196 с.

48. СтатЭксперт. Программные продукты серии «Олимп». – М.: Росэкспертиза, 1996. – 87 с.

49. Тинтнер Г. Введение в эконометрию. Пер. с немецк. - М.: Статистика, 1965. - 361 с.

50. Тинтнер Г., Фелс Э. Методы экономических исследований. - М.: Прогресс, 1971. - 151 с.

51. Тихомиров Н.П., Дорохина Е.Ю. Эконометрика: Учебник. – М.: Издательство «Экзамен», 2003. – 512 с.

52. Тюрин Ю.Н., Макаров А.А. Статистический анализ данных на компьютере. – М.: ИНФРА-М, 1998. – 528 с.

53. Уотшем Т.Дж., К. Паррамоу Количественные методы в финансах. – М.: ЮНИТИ, 1999. –527 с.

54. Финансовая математика: Математическое моделирование финансовых операций: Учеб. пособие/ под ред. В.А. Половникова и А.П. Пилипенко. – М.: Вузовский учебник, 2004. – 360 с.

55. Хеннан Э.Д. Анализ временных рядов. Пер. с англ. - М.: Наука, 1964. - 215 с.

56. Хеннан Э.Д. Многомерные временные ряды. Пер. с англ. - М.: Мир, 1974. - 575 с.

57. Химмельблау Д. Анализ процессов статистическими методами. – М.: Мир, 1973. – 957 с.

58. Четыркин Е.М. Статистические методы прогнозирования. - М.: Статистика, 1977. - 199 с.

59. Шатаев И.М. Сезонные колебания в бытовом обслуживании. -М.: Легкая индустрия, 1977. - 49 с.

60. Швырков В.В., Швыркова Т.С. Моделирование внутригодичных колебаний спроса. - М.: Статистика, 1973. - 174 с.

61. Шелобаев С.И. Математические методы и модели в экономике, финансах и бизнесе: учебное пособие. – М.: ЮНИТИ-ДАНА, 1999.

62. Шелобаев С.И. Экономико-математические методы и модели: учебное пособие для вузов – 2-е изд., перераб. и доп. – М.: ЮНИТИ-ДАНА, 2005 – 287 с.

63. Эконометрика: Учебник / Под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. - М.: Финансы и статистика, 2007. – 576 с.

64. Экономико-математические методы и прикладные модели: Учеб.пособие для вузов/ Под ред. В.В. Федосеева. – М.: ЮНИТИ, 1999. – 391 с.

Приложение 1

Значение F_α,n1,n2 – критерия Фишера – Снедекора

(n₁ – число степеней свободы для большей дисперсии;

n₂ - число степеней свободы для меньшей дисперсии)

α= 0,05
n2	n1
																		∞
	18,5	19,0	19,2	19,3	19,3	19,3	19,4	19,4	19,4	19,4	19,4	19,4	19,4	19,4	19,5	19,5	19,5	19,5	19,5
	10,1	9,55	9,28	9,12	9,01	8,94	8,89	8,85	8,81	8,79	8,74	8,70	8,66	8,64	8,62	8,59	8,57	8,55	8,53
	7,71	6,94	6,59	6,39	6,26	6,16	6,09	6,04	6,00	5,96	5,91	5,86	5,80	5,77	5,75	5,72	5,69	5,66	5,63
	6,61	5,79	5,41	5,19	5,05	4,95	4,88	4,82	4,77	4,74	4,68	4,62	4,56	4,53	4,50	4,46	4,43	4,40	4,36
	5,99	5,14	4,76	4,53	4,39	4,28	4,21	4,15	4,10	4,06	4,00	3,94	3,87	3,84	3,81	3,77	3,74	3,70	3,67
	5,59	4,74	4,35	4,12	3,97	3,87	3,79	3,73	3,68	3,64	3,57	3,51	3,44	3,41	3,38	3,34	3,30	3,27	3,23
	5,32	4,46	4,07	3,84	3,69	3,58	3,50	3,44	3,39	3,35	3,28	3,22	3,15	3,12	3,08	3,04	3,01	2,97	2,93
	5,12	4,26	3,86	3,63	3,48	3,37	3,29	3,23	3,18	3,14	3,07	3,01	2,94	2,90	2,86	2,83	2,79	2,75	2,71
	4,96	4,10	3,71	3,48	3,33	3,22	3,14	3,07	3,02	2,98	2,91	2,85	2,77	2,74	2,70	2,66	2,62	2,58	2,54
	4,84	3,98	3,59	3,36	3,20	3,09	3,01	2,95	2,90	2,85	2,79	2,72	2,65	2,61	2,57	2,53	2,49	2,45	2,40
	4,75	3,89	3,49	3,26	3,11	3,00	2,91	2,85	2,80	2,75	2,69	2,62	2,54	2,51	2,47	2,43	2,38	2,34	2,30
	4,67	3,81	3,41	3,18	3,03	2,92	2,83	2,77	2,71	2,67	2,60	2,53	2,46	2,42	2,38	2,34	2,30	2,25	2,21
	4,60	3,74	3,34	3,11	2,96	2,85	2,76	2,70	2,65	2,60	2,53	2,46	2,39	2,35	2,31	2,27	2,22	2,18	2,13
	4,54	3,68	3,29	3,06	2,90	2,76	2,71	2,64	2,59	2,54	2,48	2,40	2,33	2,29	2,25	2,20	2,16	2,11	2,07
	4,49	3,63	3,24	3,01	2,85	2,74	2,66	2,59	2,54	2,49	2,42	2,35	2,28	2,24	2,19	2,15	2,11	2,06	2,01
	4,45	3,59	3,20	2,96	2,81	2,70	2,61	2,55	2,49	2,45	2,38	2,31	2,23	2,19	2,15	2,10	2,06	2,01	1,96
	4,41	3,55	3,16	2,93	2,77	2,66	2,58	2,51	2,46	2,41	2,34	2,27	2,19	2,15	2,11	2,06	2,02	1,97	1,92
	4,38	3,52	3,13	2,90	2,74	2,63	2,54	2,48	2,42	2,38	2,31	2,23	2,16	2,11	2,07	2,03	1,98	1,93	1,88
	4,35	3,49	3,10	2,87	2,71	2,60	2,51	2,45	2,39	2,35	2,28	2,20	2,12	2,08	2,04	1,99	1,95	1,90	1,84
	4,32	3,47	3,07	2,84	2,68	2,57	2,49	2,42	2,37	2,32	2,25	2,18	2,10	2,05	2,01	1,96	1,92	1,87	1,81
	4,30	3,44	3,05	2,82	2,66	2,55	2,46	2,40	2,34	2,30	2,23	2,15	2,07	2,03	1,98	1,94	1,89	1,84	1,78
	4,28	3,42	3,03	2,80	2,64	2,53	2,44	2,37	2,32	2,27	2,20	2,13	2,05	2,01	1,96	1,91	1,86	1,81	1,76
	4,26	3,40	3,01	2,78	2,62	2,51	2,42	2,36	2,30	2,25	2,18	2,11	2,03	1,98	1,94	1,89	1,84	1,79	1,73
	4,24	3,39	2,99	2,76	2,60	2,49	2,40	2,34	2,28	2,24	2,16	2,09	2,01	1,96	1,92	1,87	1,82	1,77	1,71
	4,23	3,37	2,98	2,74	2,59	2,47	2,39	2,32	2,27	2,22	2,15	2,07	1,99	1,95	1,90	1,85	1,80	1,75	1,69
	4,21	3,35	2,96	2,73	2,57	2,46	2,37	2,31	2,25	2,20	2,13	2,06	1,97	1,93	1,88	1,84	1,79	1,73	1,67
	4,20	3,34	2,95	2,71	2,56	2,45	2,36	2,29	2,24	2,19	2,12	2,04	1,96	1,91	1,87	1,82	1,77	1,71	1,65
	4,18	3,33	2,93	2,70	2,55	2,43	2,35	2,28	2,22	2,18	2,10	2,03	1,94	1,90	1,85	1,81	1,75	1,70	1,64
	4,17	3,32	2,92	2,69	2,53	2,42	2,33	2,27	2,21	2,16	2,09	2,01	1,93	1,89	1,84	1,79	1,74	1,68	1,62
	4,08	3,23	2,84	2,61	2,45	2,34	2,25	2,18	2,12	2,08	2,00	1,92	1,84	1,79	1,74	1,69	1,64	1,58	1,51
	4,00	3,15	2,76	2,53	2,37	2,25	2,17	2,10	2,04	1,99	1,92	1,84	1,75	1,70	1,65	1,59	1,53	1,47	1,39
	3,92	3,07	2,68	2,45	2,29	2,17	2,09	2,02	1,96	1,91	1,83	1,75	1,66	1,61	1,55	1,50	1,43	1,35	1,25
∞	3,84	3,00	2,60	2,37	2,21	2,10	2,01	1,94	1,83	1,83	1,75	1,67	1,57	1,52	1,46	1,39	1,32	1,22	1,00

α= 0,01
n2	n1
																		∞
		4999,5
	98,50	99,00	99,17	99,25	99,30	99,33	99,36	99,37	99,39	99,40	99,42	99,43	99,45	99,46	99,47	99,47	99,48	99,49	99,50
	34,12	30,82	29,46	28,71	28,24	27,91	27,67	27,49	27,35	27,23	27,05	26,87	26,69	26,60	26,50	26,41	26,32	26,22	26,13
	21,20	18,00	16,69	15,98	15,52	15,21	14,98	14,80	14,66	14,55	14,37	14,20	14,02	13,93	13,84	13,75	13,65	13,56	13,46
	16,26	13,27	12,06	11,39	10,97	10,67	10,46	10,29	10,16	10,05	9,89	9,72	9,55	9,47	9,38	9,29	9,20	9,11	9,02
	13,75	10,92	9,78	9,15	8,75	8,47	8,26	8,10	7,989	7,87	7,72	7,56	7,40	7,31	7,23	7,14	7,06	6,97	6,88
	12,25	9,55	8,45	7,85	7,46	7,19	6,99	6,84	6,72	6,62	6,47	6,31	6,16	6,07	5,99	5,91	5,82	5,74	5,65
	11,26	8,65	7,59	7,01	6,63	6,37	6,18	6,03	5,91	5,81	5,67	5,52	5,36	5,28	5,70	5,12	5,03	4,95	4,86
	10,56	8,02	6,99	6,42	6,06	5,80	5,61	5,47	5,35	5,26	5,11	4,96	4,81	4,73	4,65	4,57	4,48	4,40	4,31
	10,04	7,56	6,55	5,99	5,64	5,39	5,20	5,06	4,94	4,85	4,71	4,56	4,41	4,33	4,25	4,17	4,08	4,00	3,91
	9,65	7,21	6,22	5,67	5,32	5,07	4,89	4,74	4,63	4,54	4,40	4,25	4,10	4,02	3,94	3,86	3,78	3,69	3,60
	9,33	6,93	5,95	5,41	5,06	4,82	4,64	4,50	4,39	4,30	4,16	4,01	3,86	3,78	3,70	3,62	3,54	3,45	3,36
	9,07	6,70	5,74	5,21	4,86	4,62	4,44	4,30	4,19	4,10	3,96	3,82	3,66	3,59	3,51	3,43	3,34	3,25	3,17
	8,86	6,51	5,56	5,04	4,69	4,46	4,28	4,14	4,03	3,94	3,80	3,66	3,51	3,43	3,35	3,27	3,18	3,09	3,00
	8,68	6,36	5,42	4,89	4,56	4,32	4,14	4,00	3,89	3,80	3,67	3,52	3,37	3,29	3,21	3,13	3,05	2,96	2,87
	8,53	6,23	5,29	4,77	4,44	4,20	4,03	3,89	3,78	3,69	3,55	3,41	3,26	3,18	3,10	3,02	2,93	2,84	2,75
	8,40	6,11	5,18	4,67	4,34	4,10	3,93	3,79	3,68	3,59	3,46	3,31	3,16	3,08	3,00	2,92	2,83	2,75	2,65
	8,29	6,01	5,09	4,58	4,25	4,01	3,84	3,71	3,60	3,51	3,37	3,23	3,08	3,00	2,92	2,84	2,75	2,66	2,57
	8,18	5,93	5,01	4,50	4,17	3,94	3,77	3,63	3,52	3,43	3,30	3,15	3,00	2,92	2,84	2,76	2,67	2,58	2,49
	8,10	5,85	4,94	4,43	4,10	3,87	3,70	3,56	3,46	3,37	3,23	3,09	2,94	2,86	2,78	2,69	2,61	2,52	2,42
	8,02	5,78	4,87	4,37	4,04	3,81	3,64	3,51	3,40	3,31	3,17	3,03	2,88	2,80	2,72	2,64	2,55	2,46	2,36
	7,95	5,72	4,82	4,31	3,99	3,76	3,59	3,45	3,35	3,26	3,12	2,98	2,83	2,75	2,67	2,58	2,50	2,40	2,31
	7,88	5,66	4,76	4,26	3,94	3,71	3,54	3,41	3,30	3,21	3,07	2,93	2,78	2,70	2,62	2,54	2,45	2,35	2,26
	7,82	5,61	4,72	4,22	3,90	3,67	3,50	3,36	3,26	3,17	3,03	2,89	2,74	2,66	2,58	2,49	2,40	2,31	2,21
	7,77	5,57	4,68	4,18	3,85	3,63	3,46	3,32	3,22	3,13	2,99	2,85	2,70	2,62	2,54	2,45	2,36	2,27	2,17
	7,72	5,53	4,64	4,14	3,82	3,59	3,42	3,29	3,18	3,09	2,96	2,81	2,66	2,58	2,50	2,42	2,33	2,23	2,13
	7,68	5,49	4,60	4,11	3,78	3,56	3,39	3,26	3,15	3,06	2,93	2,78	2,63	2,55	2,47	2,38	2,29	2,20	2,10
	7,64	5,45	4,57	4,07	3,75	3,53	3,36	3,23	3,12	3,03	2,90	2,75	2,60	2,52	2,44	2,35	2,26	2,17	2,06
	7,60	5,42	4,54	4,04	3,73	3,50	3,33	3,20	3,09	3,00	2,87	2,73	2,57	2,49	2,41	2,33	2,23	2,14	2,03
	7,56	5,39	4,51	4,02	3,70	3,47	3,30	3,17	3,07	2,98	2,84	2,70	2,55	2,47	2,39	2,30	2,21	2,11	2,01
	7,31	5,18	4,31	3,83	3,51	3,29	3,12	2,99	2,89	2,80	2,66	2,52	2,37	2,29	2,20	2,11	2,02	1,92	1,80
	7,08	4,98	4,13	3,65	3,34	3,12	2,95	2,82	2,72	2,63	2,50	2,35	2,20	2,12	2,03	1,94	1,84	1,73	1,60
	6,85	4,79	3,95	3,48	3,17	2,96	2,79	2,66	2,56	2,47	2,34	2,19	2,03	1,95	1,86	1,76	1,66	1,53	1,38
∞	6,63	4,61	3,78	3,32	3,02	2,80	2,64	2,51	2,41	2,32	2,18	2,04	1,88	1,79	1,70	1,59	1,47	1,32	1,00

Приложение 2

Значения t_p,n - критерия Стьюдента (двустороннего)

Число степеней свободы n	Вероятность p
0,1	0,2	0,3	0,4	0,35	0,6	0,7	0,8	0,9	0,95	0,98	0,99
	0,16	0,32	0,51	0,73	1,00	1,38	1,96	3,08	6,31	12,71	31,82	63,66
	0,14	0,29	0,44	0,62	0,82		1,34	1,89	2,92	4,30	6,96	9,92
	0,14	0,28	0,42	0,58	0,76	0,98	1,25	1,64	2,35	3,18	4,54	5,84
	0,13	0,27	0,41	0,57	0,74		1,19	1,53	2,13	2,78	3,75	4,60
	0,13	0,27	0,41	0,56	0,73		1,16	1,48	2,01	2,57	3,36	4,03
	0,13	0,26	0,40	0,55	0,72	0,91	1,13	1,44	1,94	2,45	3,14	3,71
	0,13	0,26	0,40	0,55	0,71	0,90	1,12	1,41	1,89	2,36	3,00	3,50
	0,13	0,26	0,40	0,50	0,70	0,89	1,11	1,40	1,86	2,31	2,90	3,35
	0,13	0,26	0,40	0,54	0,70	0,88	1,10	1,38	1,83	2,26	2,82	3,25
	0,13	0,26	0,40	0,54	0,70	0,88	1,09	1,37	1,81	2,23	2,76	3,17
	0,13	0,26	0,40	0,54	0,70	0,88	1,09	1,36	1,80	2,20	2,72	3,11
	0,13	0,26	0,39	0,54	0,69	0,87	1,08	1,36	1,78	2,18	2,68	3,05
	0,13	0,26	0,39	0,54	0,69	0,87	1,08	1,35	1,77	2,16	2,65	3,01
	0,13	0,26	0,39	0,54	0,69	0,87	1,08	1,34	1,76	2,14	2,62	2,98
	0,13	0,26	0,39	0,54	0,69	0,87	1,07	1,34	1,75	2,13	2,60	2,95
	0,13	0,26	0,39	0,53	0,69	0,86	1,07	1,34	1,75	2,12	2,58	2,92
	0,13	0,26	0,39	0,53	0,69	0,86	1,07	1,33	1,74	2,11	2,57	2,90
	0,13	0,26	0,39	0,53	0,69	0,86	1,07	1,33	1,73	2,10	2,55	2,88
	0,13	0,26	0,39	0,53	0,69	0,86	1,07	1,33	1,73	2,09	2,54	2,86
	0,13	0,26	0,39	0,53	0,69	0,86	1,06	1,32	1,72	2,09	2,53	2,84
	0,13	0,26	0,39	0,53	0,69	0,86	1,06	1,32	1,72	2,08	2,52	2,83
	0,13	0,26	0,39	0,53	0,69	0,86	1,06	1,32	1,72	2,07	2,51	2,82
	0,13	0,26	0,39	0,53	0,68	0,86	1,06	1,32	1,71	2,07	2,50	2,81
	0,13	0,26	0,39	0,53	0,68	0,86	1,06	1,32	1,71	2,06	2,49	2,80
	0,13	0,26	0,39	0,53	0,68	0,86	1,06	1,32	1,71	2,06	2,48	2,79
	0,13	0,26	0,39	0,53	0,68	0,86	1,06	1,31	1,71	2,06	2,48	2,78
	0,13	0,26	0,39	0,53	0,68	0,85	1,06	1,31	1,70	2,05	2,47	2,77
	0,13	0,26	0,39	0,53	0,68	0,85	1,06	1,31	1,70	2,05	2, 47	2,76
	0,13	0,26	0,39	0,53	0,68	0,85	1,05	1,31	1,70	2,04	2,46	2,76
	0,13	0,26	0,39	0,53	0,68	0,85	1,05	1,31	1,70	2,04	2,46	2,75
	0,13	0,25	0,39	0,53	0,68	0,85	1,05	1,30	1,68	2,02	2,42	2,70
	0,13	0,25	0,39	0,53	0,68	0,85	1,05	1,30	1,67	2,00	2,39	2,66
	0,13	0,25	0,39	0,53	0,68	0,84	1,04	1,29	1,66	1,98	2,36	2,62
∞	0,13	0,25	0,38	0,52	0,67	0,84	1,04	1,28	1,64	1,96	2,33	2,58

Приложение 3

Значения d₁ и d₂ критерия Дарбина – Уотсона

при уровне значимости α= 0,05

(n - число наблюдений; m - число объясняющих переменных)

n	m=1	m=2	m=3	m=4	m=5
d1	d2	d1	d2	d1	d2	d1	d2	d1	d2
	0,61	1,40	-	-	-	-
	0,70	1,36	0,47	1,90	-	-
	0,76	1,33	0,56	1,78	0,37	2,29
	0,82	1,32	0,63	1,70	0,46	2,13
	0,88	1,32	0,70	1,64	0,53	2,03
	0,93	1,32	0,66	1,60	0,60	1,93
	0,97	1,33	0,81	1,58	0,66	1,86
	1,01	1,34	0,86	1,56	0,72	1,82
	1,05	1,35	0,91	1,55	0,77	1,78
	1,08	1,36	0,95	1,54	0,82	1,75	0,69	1,97	0,56	2,21
	1,10	1,37	0,98	1,54	0,86	1,73	0,74	1,93	0,62	2,15
	1,13	1,38	1,02	1,54	0,90	1,71	0,78	1,90	0,67	2,10
	1,16	1,39	1,05	1,53	0,93	1,69	0,82	1,87	0,71	2,06
	1,18	1,40	1,08	1,53	0,97	1,68	0,86	1,85	0,75	2,02
	1,20	1,41	1,10	1,54	1,00	1,68	0,90	1,83	0,79	1,99
	1,22	1,42	1,13	1,54	1,03	1,67	0,93	1,81	0,83	1,96
	1,24	1,43	1,15	1,54	1,05	1,66	0,96	1,80	0,86	1,94
	1,26	1,44	1,17	1,54	1,08	1,66	0,99	1,79	0,90	1,92
	1,27	1,45	1,19	1,55	1,10	1,66	1,01	1,78	0,93	1,90
	1,29	1,45	1,21	1,55	1,12	1,66	1,04	1,77	0,95	1,89
	1,30	1,46	1,22	1,55	1,14	1,65	1,06	1,76	0,98	1,88
	1,32	1,47	1,24	1,56	1,16	1,65	1,08	1,76	1,01	1,86
	1,33	1,48	1,26	1,56	1,18	1,65	1,10	1,75	1,03	1,85
	1,34	1,48	1,27	1,56	1,20	1,65	1,12	1,74	1,05	1,84
	1,35	1,49	1,28	1,57	1,21	1,65	1,14	1,74	1,07	1,83
	1,36	1,50	1,30	1,57	1,23	1,65	1,16	1,74	1,09	1,83
	1,37	1,50	1,31	1,57	1,24	1,65	1,18	1,73	1,11	1,82
	1,38	1,51	1,32	1,58	1,26	1,65	1,19	1,73	1,13	1,81
	1,39	1,51	1,33	1,58	1,27	1,65	1,21	1,73	1,15	1,81
	1,40	1,52	1,34	1,58	1,28	1,65	1,22	1,73	1,16	1,80
	1,41	1,52	1,35	1,59	1,29	1,65	1,24	1,73	1,18	1,80
	1,42	1,53	1,36	1,59	1,31	1,66	1,25	1,72	1,19	1,80
	1,43	1,54	1,37	1,59	1,32	1,66	1,26	1,72	1,21	1,79
	1,43	1,54	1,38	1,60	1,33	1,66	1,27	1,72	1,22	1,79
	1,44	1,54	1,39	1,60	1,34	1,66	1,29	1,72	1,23	1,78
	1,48	1,57	1,43	1,62	1,38	1,67	1,34	1,72	1,29	1,77
	1,50	1,59	1,46	1,63	1,42	1,67	1,38	1,72	1,34	1,77
	1,53	1,60	1,49	1,64	1,45	1,68	1,41	1,72	1,38	1,77
	1,55	1,62	1,51	1,65	1,48	1,69	1,44	1,73	1,41	1,77
	1,57	1,63	1,54

Дата добавления: 2014-10-22