Геометрическая иллюстрация к формуле (1)

Смысл формулы (1) можно также проиллюстрировать вычислением объема цилиндроида, зная формулу для вычисления объема тела с известной площадью поперечного сечения: 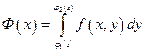— это площадь поперечного сечения цилиндроида плоскостью . Тогда с помощью определенного интеграла находим весь объем: .

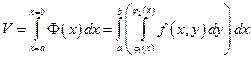Пример 1 (вычисление двойного интеграла в декартовых координатах)

Вычислить 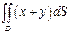, если область D ограничена линиям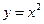и и

Решение

Строим область D, определяем её правильность в направлении оси 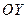и записываем системой неравенств

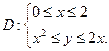
Вычисляем данный двойной интеграл сведением его к повторному интегралу по формуле (1):

.

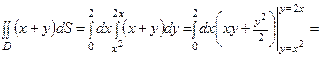
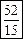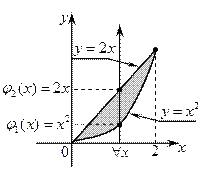
Вариант 2 (для области правильной в направлении оси OX)

Если область D — правильная в направлении оси OX, то она записывается системой неравенств 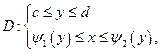в которой отражено, что переменная y изменяется в постоянных пределах, а переменная x изменяется, вообще говоря, в переменных пределах,

зависящих от y; при этом геометрически отрезок является проекцией области D на ось 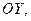линия ограничивает область D слева, линия ограничивает область справа (Рис. 4).

Тогда двойной интеграл сводится к повторному по формуле

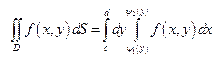
(2)

Справа стоит повторный интеграл, в котором внутренний интеграл вычисляется по переменной x в предположении, что y является постоянной; результатом вычисления внутреннего интеграла является некоторая функция 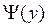. Затем вычисляется внешний интеграл от 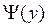по переменной y в постоянных пределах, в результате получается число.

Пример 2 (вычисление двойного интеграла в декартовых координатах)

Вычислить 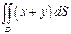, если область D ограничена линиями и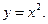

Решение

Область D, уже построенная в предыдущем примере, является также правильной в направлении оси поэтому может быть записана системой неравенств

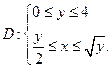
Вычисляем данный двойной интеграл сведением его к повторному по формуле (2):

.

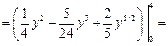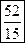2.2. Задача об изменении порядка интегрирования в повторном интеграле (Как изменяется порядок интегрирования в повторном интеграле?)

На применении формул (1) и (2) для одной и той же области основано решение задачи об изменении порядка интегрирования в повторном интеграле. Рассмотрим пример такой задачи.

Пусть дан повторный интеграл и требуется изменить порядок интегрирования так, чтобы внешний интеграл вычислялся бы по переменной y, а внутренний – по переменной x.

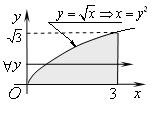
По пределам в данном повторном интеграле восстанавливаем область D, записывая для нее систему неравенств

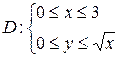
Далее строим область D по этой системе неравенств и записываем её неравенствами другим способом, так чтобы в постоянных пределах изменялась переменная y:

Теперь переходим от исходного повторного интеграла к двойному интегралу по области D, а затем снова сводим двойной интеграл к повторному, но с другим порядком интегрирования:

Ответ: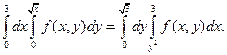

Задача об изменении порядка интегрирования имеет практическое значение в связи с возможными трудностями при вычислении повторных интегралов от функции f (x, y).

Дата добавления: 2014-10-15