
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Співвідношення механіки суцільного середовища
|
|
|
|
Поняття про механіку суцільного середовища
Основні положення статистичної геомеханіки при визначенні стійкості виробок, укосів і бортів кар'єру
Основу механіки суцільного середовища становлять подання про матеріальні тіла як «про деяку субстанцію, що безупинно заповнює обсяг геометричного простору» і наділеного певними фізичними властивостями, що відбивають статистичні закономірності для реальних фізичних середовищ.
Уведене припущення про сплошности середовища дозволяє наділяти нескінченно малі обсяги тіл властивостями середовища й ефективно використати аналітичний апарат диференціального й інтегрального вирахування. Зокрема, напруги й переміщення окремих крапок середовища, можливо, представляти у вигляді деяких функцій координат і часу, похідних (безперервних і дифференцируемых), які забезпечили б потребуючу точність рішення завдання.
У механіки суцільних середовищ різні дві категорії сил: зовнішні й внутрішні.
Зовнішні сили – поверхневі й об'ємні. Поверхневі, наприклад тиск, прикладений до поверхні тіла й конкретна взаємодія, що характеризує, його з ін. тілами. Об'ємні (масові) прикладені до внутрішніх частин тіла - сили ваги, сили інерції й ін.
Внутрішні сили – це сили зв'язку між окремими частками речовини. Внутрішні сили під впливом зовнішніх змінюються, одержують збільшення, які і є основним предметом вивчення механіки деформації тел.
Зовнішні й внутрішні сили характеризуються інтенсивністю, що називається напругою.
Напруга й деформації елементарного обсягу є функціями координат, тобто трьома складовими напруг  (
( ;
; 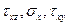 ;
;  ) обумовлених дев'ятьма компонентами.
) обумовлених дев'ятьма компонентами.
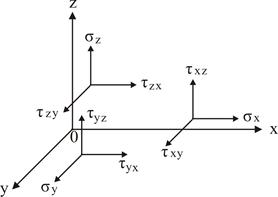
Деформація (повна e) подібно напрузі може бути також представлена у вигляді трьох взаємно перпендикулярних складових. Одна з них спричиняється лінійні деформації тіла Ɛ (подовження або вкорочення), а дві інші перпендикулярні до неї й відповідають сдвиговим деформаціям γ.
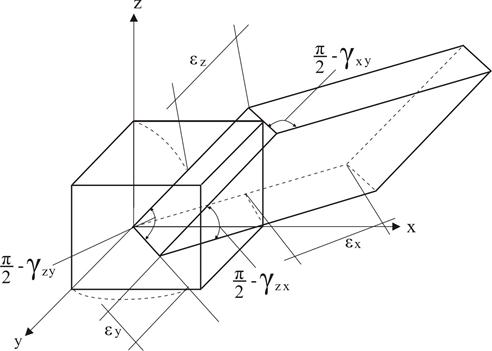
Тобто деформування будь-якого обсягу можна охарактеризувати деформаціями трьох взаємно перпендикулярних відрізків. Тому деформований стан якого-небудь обсягу могло бути однозначно визначено дев'ятьма компонентами.
Дев'ять компонентів напруг і деформацій становлять тензори напруг і деформацій у даній крапці.
 ;
; 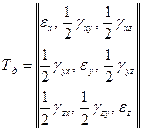 (1)
(1)
Якщо скласти рівняння моментів всіх сил щодо кожної з осей Ох, Оy, Oz виділеного деформуючого обсягу й прирівняти їх до нуля, то легко можна вивести:
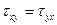 ;
; 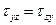 ;
; 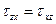 ;
;
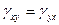 ;
; 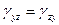 ;
;  (2)
(2)
Тому число необхідних величин для певного напружено-деформаційного стану в крапці скорочується до шести.
Умова рівноваги будь-якої внутрішньої крапки деформованого тіла можна записати у вигляді:
 (3)
(3)
де  – проекції масових сил на осі Ох, Оy, Oz.
– проекції масових сил на осі Ох, Оy, Oz.
Для крапок поверхні розглянутого тіла керування рівноваги має вигляд:
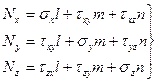 (4)
(4)
де  – проекції зовнішніх сил на нормаль до поверхні деформованого тіла;
– проекції зовнішніх сил на нормаль до поверхні деформованого тіла;
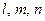 – напрямного косинуса нормалі.
– напрямного косинуса нормалі.
Останнє рівняння характеризує зв'язок між зовнішніми силами, що діють на поверхні тіла, і компонентами напруг, що діють усередині тіла в поверхні.
Однак, щоб сплошность середовища й після деформування не змінювалася, співвідношення компонентів деформацій повинне задовольняти умовам нерозривності деформацій.
Пружна модель ґрунтується на прямій пропорційно між напругою й деформаціями (Законі Гука). Зв'язок компонентів напруги й компонентів деформацій має вигляд:
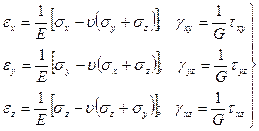 (5)
(5)
де 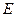 – модуль пружності;
– модуль пружності;
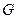 – модуль зрушення;
– модуль зрушення;
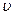 – коефіцієнт Пуассона або поперечної деформації.
– коефіцієнт Пуассона або поперечної деформації.
Плоский напружений стан ( характерно для тонких шарів, навантажених по контурі силами, паралельними їхньої площини).
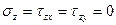 ;
;
Тензор напруг має вигляд:
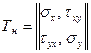
Тензор деформацій містить компоненту лінійної деформації 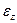 , вона визначається рівнянням (відповідно до вираження (5)):
, вона визначається рівнянням (відповідно до вираження (5)):
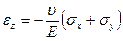

Наприклад, якщо по контурі вертикального стовбура в масиві порід виділити тонкий шар перпендикулярний до осі стовбура, то він буде перебувати в гравітаційному полі сил і напружений стан порід у цьому шарі можна думати плоским.
Умова плоскої деформації (виникає у випадку, коли переміщення крапок деформованого об'єкта відбуваються тільки в одній площині). 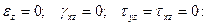
Тензор деформацій може бути записаний:

Т. к. 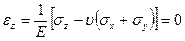
те 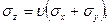
тоді для умов плоскої деформації тензор напруг визначиться вираженням
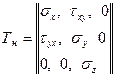
У гравітаційному полі сил в умови плоскої деформації перебувають породи навколо перетину горизонтального гірського виробки.
При наявності пружної-пластичної моделі до загальних 9 рівнянням необхідно додати шість фізичних рівнянь
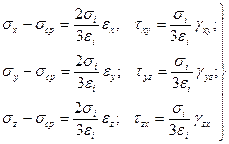
де 

 .
.
Залежність м.  і
і 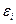 виражається рівнянням
виражається рівнянням 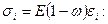
Вид функції 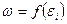 встановлюється по випробуваннях порід при одноосьовому стисненні-розтяганні.
встановлюється по випробуваннях порід при одноосьовому стисненні-розтяганні.
|
|
|
|
|
Дата добавления: 2014-10-22; Просмотров: 332; Нарушение авторских прав?; Мы поможем в написании вашей работы!