Постановка обобщенной задачи замены КСНО

Выбор оптимальных сроков службы КСНО и его элементов

При создании КСНО одним из важных является вопрос о целесообразности разработки нового комплекса или его элементов взамен существующего. Решение такой задачи дает ответ на начальной стадии проектирования на вопрос, стоит ли начинать разработку нового КСНО или каких-то его элементов или целесообразнее воспользоваться существующим комплексом.

Поскольку вновь созданные технические устройства более эффективны, чем старые, но требуют больших затрат на разработку и производство, то, очевидно, существуют оптимальные сроки разработки КСНО (или элементов) новых типов.

Сформировать такую задачу можно следующим образом. Определить оптимальные сроки разработки нового КСНО и замены им старого при условии, что показатель эффективности КСНО (например, суммарные затраты на заданный период) будет минимальным и в любой момент будет обеспечено необходимое качество работы, которую необходимо выполнить данному КСНО. Считается, что сразу же после разработки новый комплекс поступает в производство, а производство комплекса старого типа прекращается. Кроме того, разработка нового КСНО начинается тогда, когда до конца рассматриваемого периода ее можно завершить.

Математически эта задача формулируется следующим образом.

Определить совокупность 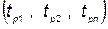,включая число разработок n, при которой с учетом условия

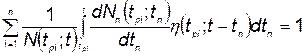(5.43)

обеспечивается минимум суммарных затрат на комплексы всех типов с учетом приведения затрат к единому моменту времени:

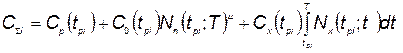(5.44)

или

(5.45)

где 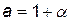; 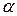— коэффициент эффективности капиталовложений; 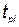— время конца разработки КСНО нового типа (i -гo типа); 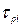— время, затрачиваемое на разработку 1-го нового комплекса; 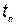— время производства нового комплекса; 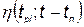— функция живучести, характеризующая процесс хранения и эксплуатации; N_ni — количество произведенных комплексов i -го типа; 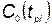и 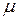— коэффициенты; 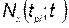— количество устройств j' -ro типа, разработка которого закончена к моменту 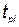; 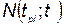— функция потребности в устройстве i -го типа; t — текущее время; 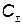— суммарные затраты, которые складываются из затрат на разработку комплексов всех типов, на производство, хранение и эксплуатацию; 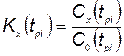;;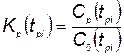 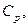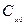— затраты на разработку и хранение соответственно; 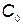— коэффициент. Следует отметить, что рассмотренный процесс не является марковским, поскольку затраты на данный год зависят от предыстории, т. е. от времени производства нового комплекса. В связи с этим для решения подобной задачи метод динамического программирования не может быть использован.

Рассмотрим несколько частных случаев решения поставленной задачи.

Дата добавления: 2014-10-15