Выбор оптимальных сроков службы элемента КСНО для частного случая

Рассмотрим случай:

1) живучесть комплекса задана функцией , т. е. выходом элементов комплекса из строя по мере хранения и эксплуатации можно пренебречь; 2) функция потребности описывается выражением вида

; , (5.46)

где N₀ — коэффициент; t — текущее время; 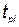— время конца разработки комплекса или элемента КСНО i -го типа;

2) стоимость производства КСНО не зависит от размера партии и времени его разработки, а стоимость разработки КСНО не зависит от времени конца разработки, т.е. функция суммарных затрат описывается выражением

. (5.47)

Если рассматривать первую разработку, то уравнение (5.47) запишется в следующем виде:

. (5.48)

Возьмем производную по 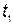и приравняем ее нулю:

. (5.49)

Откуда оптимальное значение

, (5.50)

где ; — принятый момент начала отсчета; 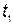— время

конца первой разработки; 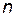— количество новых разработок.

Подставляя 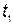, определяемое по формуле (5.50), в выражение суммарной стоимости (5.47), получаем выражение минимальных суммарных затрат, складывающихся из затрат на разработку, их производство, хранение и эксплуатацию:

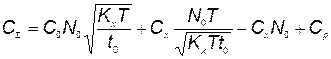. (5.51)

Аналогичным образом решается задача при второй, третьей и других разработках.

Если всего есть 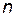новых разработок, то формулы (5.50) и (5.51) принимают соответственно вид

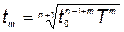,(5.52)

где т — номер разработки,

. (5.53)

Обозначив и , а также продифференцировав (5.53) по 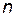и приравняв производную нулю, получим

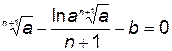.(5.54)

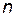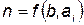В результате решения этого уравнения находится оптимальная величина . Это уравнение может быть решено графически (рис. 5.2), если задаваться значениями и строить график по уравнению (5.54).

Поскольку 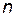может быть только положительной и иметь только целые значения, то значения, полученные с помощью графика, следует округлять в большую и меньшую стороны до целого числа и рассчитывать суммарные затраты для этих двух значений, выбирая из них то при котором будет наименьшим.

Следует отметить, что замена комплекса (или его элементов) с большим сроком живучести целесообразна при большом выигрыше в эффективности нового КСНО по сравнению с комплексом старого типа, т. е. моральное старение комплекса с большим сроком живучести происходит медленнее, чем комплекса с малыми сроками живучести.

Дата добавления: 2014-10-15