Общая постановка задачи оптимизации надежности КСНО

Выбор оптимальной надежности КСНО и его элементов

Повышение надежности КСНО снижает расходы, связанные эксплуатацией, а также уменьшает потребность в резервировании КСНО или его элементов. С другой стороны, для создания НО с большей надежностью требуются дополнительные затраты, связанные с его разработкой и производством. Эти затраты могут быть существенными. Поэтому, очевидно, существует оптимальная надежность КСНО, определяемая из условия минимизации затрат на выполнение поставленных перед комплексом задач.

Общая задача выбора оптимальной надежности КСНО и путей ее обеспечения может быть сформулирована следующим образом.

Требуется выбрать такие проектные параметры КСНО

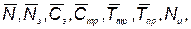(5.62)

при которых суммарные затраты минимизируются, т. е.

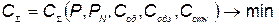, (5.63)

при выполнении дисциплинирующих условий, связывающих стоимость и надежность с проектными параметрами

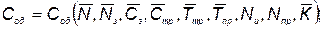
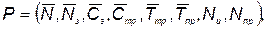(5.64)

и ограничений по массе и габаритам

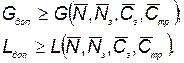(5.65)

Здесь приняты следующие обозначения: 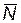— вектор с компонентами ; — количество i -х элементов, повышающих надежность за счет резервирования; 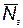— вектор с компонентами 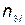; 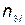— количество запасных элементов, замена которых происходит достаточно быстро; 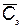— вектор стоимости элементов; 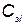— стоимость i –го элемента; 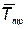— вектор с компонентами 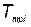, где 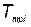— время тренировки i –го элемента; 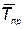— вектор с компонентами 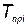, где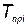— время работы

i –го элемента до замены в процессе профилактических работ; N_и — число испытаний КСНО в процессе отработки; 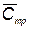— вектор с компонентами 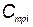, где 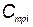— стоимость поддержания температурного режима i -го элемента; Р — надежность КСНО; 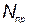— общее количество произведенных КСНО;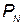- вероятность выполнения поставленной задачи при использовании 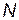комплексов, которая определяется по формуле 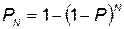; 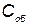— затраты на однократное применение КСНО; 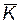— вектор коэффициентов связывающих стоимость с техническими характеристиками КСНО; 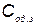— затраты на содержание одного резервного КСНО; 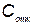— дополнительные затраты, связанные с отказом комплекса.

В зависимости от особенностей функционирования КСНО могут быть наложены ограничения на его массу (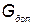) и габаритные размеры ().

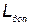Рассмотрим выбор оптимальной надежности на простейшем примере. Пусть в КСНО присутствует агрегат, стоимость приобретения которого 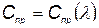, где 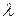— интенсивность отказов. Будем считать, что время отказов имеет экспоненциальное распределение. Стоимость одного часа эксплуатации агрегата, независимо от того, ремонтируется он или работает, .

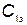Требуется определить оптимальную надежность агрегата, если стоимость приобретения агрегата определяется по формуле

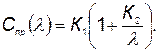(5.66)

Поскольку время отказов имеет экспоненциальное распределение, то вероятность безотказной работы за время Т будет

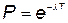, (5.67)

причем среднее время между отказами

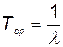, (5.68)

а среднее число отказов за время Т

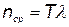. (5.69)

Полезное время работы агрегата за время Т будет

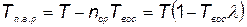, (5.70)

где 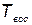— среднее время восстановления одного отказа.

Суммарные затраты на один час работы агрегата будут

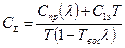. (5.71)

Подставив вместо 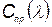его значение из (5.66), будем иметь

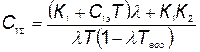. (5.72)

Для выбора оптимальной надежности (вероятности безотказной работы) необходимо найти такое 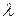, которое обращает функцию затрат 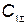в минимум, а затем полученное значение 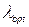подставить в формулу (5.67).

Взяв производную 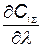и приравняв ее нулю, найдем оптимальное значение

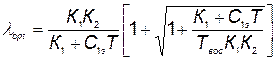. (5.73)

Подставляя значение 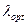из (5.73) в (5.67), получаем оптимальное значение вероятности безотказной работы агрегата:

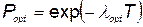. (5.74)

Дата добавления: 2014-10-15