Некоторые законы распределения дискретной случайной величины

Для дисперсии случайной величины, справедлива формула

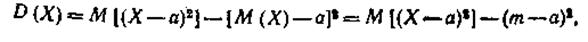
где а —произвольное число.

Этой формулой часто пользуются для вычисления дисперсии случайной величины, так как вычисление по этой формуле обычно проще, чем по формулам а) и б).

Средним квадратическим отклонением случайной величины X называется величина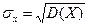

Пример №1. Случайная величина X характеризуется рядом распределения:

Определить математическое ожидание и дисперсию.

Решение. Находим математическое ожидание: М(Х) = 0-0,2+ 1-0,4 + 2-0,3 + 3-0,08 + 4.0,02 = 1,32.

Дисперсию найдем по формуле D(X) = M[(X —а)²] — М(Х)— а]², положив

а = 2; отсюда М(Х)—а = 1,32—2 = —0,68.

Составляем таблицу:

Теперь находим

Итак,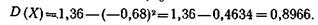

дисперсия D (X) = 0,8966; отсюда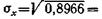0,95.

Биноминальное распределение (формула Бернулли).

В основе вывода формулы Бернулли лежит предположение, что вероятность появления события Х в испытании известна и не изменяется от испытания к испытанию.

Обозначим эту вероятность через р. Тогда вероятность непоявления события Х обозначим через qи она равна q=1-р. Зная вероятность появления события в единичном испытании, найдем вероятность Р_n(m)того, что в серии из nнезависимых испытаний это событие произойдет mраз.

, где n! = 1·2·3·…·n – факториал числа n, причем 0! = 1.

Данное выражение называется биноминальным распределением или формулой Бернулли.

Пример: появление колонии микроорганизмов данного вида в определенных условиях оценивается вероятностью р = 0,7. составить биноминальное распределение вероятностей появления колонии микроорганизмов в шести наугад взятых пробах.

Р = 0,7; q = 1-0,7 = 0,3; n = 6; m = 0,1,2,3,4,5,6.

Запишем распределение в виде таблицы:

Х
Р6(Х)	0,0007	0,01	0,057	0,18	0,32	0,3	0,11

Данное биноминальное распределение можно изобразить графически. Наибольшую вероятность имеет значение случайной величины примерно равное математическому ожиданию данной случайной величины. М(Х) = n·p = 6·0,7 = 4,2

Нормальное распределение.

При больших n использование формулы Бернулли связано с трудоемкими вычислениями (т.к., например, 20! - это число, состоящее из 19 цифр). В подобных случаях применяют формулу Лапласа – Гаусса, которая имеет вид: , где

е = 2,718 это распределение называют нормальным распределением.

Распределение Пуассона. Если вероятность появления в единичном испытании интересующего нас события очень мала, то при больших n биноминальное распределение переходит не в нормальное распределение, а в распределение Пуассона: Это распределение также называют законом распределения редких явлений.

Пример: пусть известно, что в ведре воды имеется 10000 бактерий. Вероятность нахождения бактерии в случайным образом выбранной капле р=0,001. найти распределение вероятностей количества бактерий Х в наугад взятой капле.

При хорошем перемешивании воды, в которой бактерии считаются точками, можно применить распределение Пуассона с параметрами M = np = 10000·0.001=10. вероятность того, что в капле не найдется ни одной бактерии, вычисляем по формуле:

. Вероятность того, что в капле будет 1,2,3 бактерии:

;;

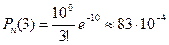
Закон распределения количества бактерий в наугад взятой капле можно представить в виде таблицы:

Х

Рn(X)10^-4

0,5

Данное распределение Пуассона можно изобразить графически. Наибольшую вероятность имеет значение случайной величины примерно равное математическому ожиданию данной случайной величины. M = np = 10

Контрольные вопросы:

Сформулируйте определение случайной величин ы.

Какая случайная величина называется дискретной?

Сформулируйте закон распределения случайной величины.

Сформулируйте определение математического ожидания случайной величины.

Сформулируйте определение дисперсии случайной величины.

Сформулируйте определение среднего квадратичного отклонения случайной величины.

Домашнее задание

Заполните в рабочей тетради занятие 11-12.

Дата добавления: 2014-10-22