Соотношение, устанавливающее тем или иным способом связь между возможными значениями случайной величины и их вероятностями, называется законом распределения случайной величины

Закон распределения дискретной случайной величины обычно задается рядом распределения:

Хi	Х1	Х2	Х3	….	Хn
pi	P1	P2	P3	….	pn

При этом 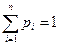, где суммирование распространяется на все (конечное и бесконечное) множество возможных значений данной случайной величины Х.

Закон распределения непрерывной случайной величины удобно задавать при помощи так называемой функции плотности вероятности f(x). Вероятность

Р (а<X<b) того, что значение, принятое случайной величиной Х, попадает в промежуток (а,b), определяется равенством

Р (а<X<b) = .

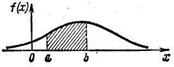
График функции f(x) называется кривой распределения.

Геометрически вероятность попадания случайной величины в промежуток (а,b) равна площади соответствующей криволинейной трапеции, ограниченной кривой распределения, осью Ох и прямыми х = а, х = b.

Функция плотности вероятности f(x) обладает следующими свойствами:

1) f(x) ≥0, 2)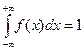

(если все значения случайной величины Х заключены в промежутке (А,В), то последнее условие может быть заменено условием ).

Рассмотрим теперь функцию F(x) = Р(Х<x). Эта функция называется функцией распределения вероятности случайной величины Х.

Функция F(x) существует как для дискретных, так и для непрерывных случайных величин. Если f(x) – функция плотности распределения вероятности непрерывной случайной величины Х, то

F(x) = .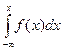

Из последнего равенства следует, что f(x) = .

Иногда функцию f(x) называют дифференциальной функцией распределения вероятности, а функцию F(x) – интегральной функцией распределения вероятности.

Отметим важнейшие свойства функции распределения вероятности:

1) F(x)- неубывающая функция своего аргумента,

2) F (- ∞) = 0.

3) F (+∞) =1

1. Математическим ожиданием дискретной случайной величины называется сумма произведений значений случайной величины на вероятности этих значений.

Если случайная величина X характеризуется конечным рядом распределения:

,

то математическое ожидание М (X) определится по формуле

M(X) = x₁p₁+-x₂ p₂+...+x_n p_n, или

Понятие математического ожидания распространяется и на непрерывную случайную величину.

Пусть f(x) — плотность вероятности случайной величины X. Тогда математическое ожидание непрерыв ной случайной величины X определяется равенством

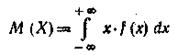
(при условии, что значение этого интеграла конечно).

Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

Дисперсия случайной величины есть мера рассеяния ее значений около ее математического ожидания.

Само слово дисперсия означает «рассеивание».

Если ввести обозначение М (Х) = т, то формулы для вычисления дисперсии примут следующий вид:

а)для дискретной случайной величины X:

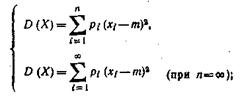
б) для непрерывной случайной величины X:

Дата добавления: 2014-10-22