Сочетания

Конечные упорядоченные подмножества, содержащие по m элементов, выбранных из n элементов по m элементов основного множества, называются размещениями из n элементов по m элементов.

Размещения.

Пусть дано некоторое конечное множество А, состоящее из n различных элементов. Выберем некоторым образом из n элементов m различных элементов, и

будем составлять из этих m элементов различные упорядоченные множества.

Число всех возможных размещений из n элементов по m элементов обозначается 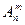_. Число размещений из n элементов по m можно записать в виде формулы: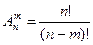

Пример: Группа учащихся изучает 7 учебных дисциплин. Сколькими способами можно составить расписание занятий в понедельник, если в этот день недели должно быть 4 различных урока?

Решение. Число способов равно числу размещений из 7 элементов по 4, т.е. равно А⁴₇ =7·6·5·4=840

Число размещений и число перестановок связаны формулой:

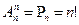
Конечные неупорядоченные множества, содержащие m различных элементов, выбранных из n элементов заданного множества, называются сочетаниями из n элементов по m элементов. Обозначается 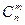или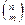

Число 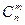различных неупорядоченных множеств, содержащих по m различных элементов, выбранных из элементов, будет вычисляться по формуле: =

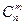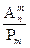
Используя формулы для подсчета числа перестановок Р_m и числа размещений 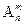, получим =

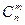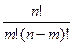
Пример: группу учащихся колледжа должна экзаменовать по математике комиссия, состоящих из 7 человек. Сколькими способами может быть составлена комиссия, если в колледже 14учителей математики?

Решение: используем формулу подсчета числа сочетаний = .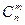

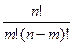Здесь n=14, а m = 7, тогда = .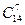

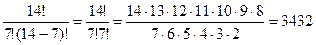Для числа сочетаний справедливы равенства:

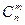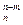
= С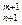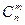, С= + С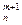, а также С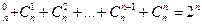

.Последнее свойство иногда формулируется в виде следующей теоремы о конечных множествах: Число всех подмножеств множества, состоящего из n элементов, равно 2ⁿ.

Контрольные вопросы:

Дайте определение числовой последовательности.

Перечислите способы задания последовательностей.

Какие последовательности называют ограниченными?

Сформулируйте определение предела числовой последовательности.

Сформулируйте необходимые и достаточное условия сходимости последовательности.

Дайте определение предела функции в точке.

Перечислите основные теоремы о пределах функции в точке.

Сформулируйте определение числового ряда.

Какой ряд называется сходящимся, расходящимся?

Сформулируйте необходимое условие сходимости ряда.

Сформулируйте признак Даламбера сходимости рядов.

Какой ряд называют абсолютно сходящимся?

Какой ряд называют условно сходящимся?

Запишите формулу разложения функции в ряд Маклорена.

Понятие множества, элемента множества, подмножества.

Способы обозначения и задания множества.

Понятие равных множеств, пустого множества.

Пересечение множеств. Непересекающиеся множества.

Переместительный и сочетательный законы.

Сумма (объединение) множеств.

Разность множеств. Дополнение до множества.

Прямое произведение множеств.

Эквивалентные множества. Взаимно однозначное соответствие

Сформулируйте определение графа.

Перечислите способы задания графов.

Сформулируйте определение комбинаторики, как раздела математики.

Сформулируйте определение факториала.

Сформулируйте определение перестановок.

Дайте понятие размещения и сочетания.

Домашнее задание

Заполните в рабочей тетради занятие 7. 8, 9, 10

Лекция № 5

.

Тема: Основные понятия теории вероятности и математической статистики

План:

Дата добавления: 2014-10-22