Выборочные характеристики

В математической статистике вводятся числовые характеристики выборки аналогично числовым характеристикам случайных величин в теории вероятности.

Пусть имеется выборка, объема n.

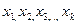
Выборочным математическим ожиданием (выборочным средним) называют среднее арифметическое значение выборки.

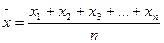
Если выборка задана статистическим рядом, то:

Выборочной дисперсией называют среднее арифметическое квадратов отклонений значений выборки от выборочного среднего.

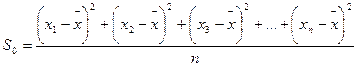
Если выборка задана статистическим рядом, то:

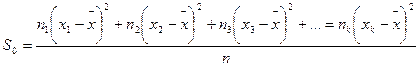
Несмещенная выборочная дисперсия:

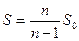
Пример: Дана выборка 1, 2, 3, 4, 5. Найти выборочное среднее x, выборочную дисперсию 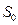, несмещенную выборочную дисперсию S. Объем выборки n =5

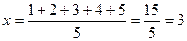
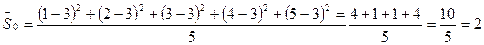
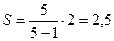
Санитарная (медицинская) статистика является одной из основных отраслей статистической науки и важнейшим методическим разделом социальной гигиены и организации здравоохранения.

В задачи санитарной статистики входят:

1. определение уровня и сдвигов в здоровье отдельных групп населения;

2.оценка влияния социально-биологических факторов на здоровье населения;

3. анализ данных о сети, кадрах, деятельности лечебно-профилактических учреждений;

4. определение эффективности лечебно-профилактических мероприятий;

5. использование статистических методов в экспериментальных, клинико-биологических, социально-гигиенических исследованиях.

Важнейшим принципом статистики является применение ее для изучения не единичных, а массовых явлений, объединенных в группы для выявления общих свойств и закономерностей. Эти закономерности, как правило не могут быть обнаружены при наблюдении за единичными явлениями, а проявляются в массе наблюдений

Статистическая совокупность, её элементы, признаки.

Статистическая совокупность – группа, состоящая из множества относительно однородных элементов (единиц наблюдения). Например, группа оперированных, население на участке, больные стационара, новорожденные на данном участке, пациенты поликлиники, больные на дому и т.д..

Единица наблюдения – каждое отдельное явление, подлежащее учету, наделенное признаками сходства.

В большинстве социально- гигиенических исследований учитываемыми признаками является: пол, возраст, семейное положение, уровень образования, доход и размеры жилплощади на одного человека, масса тела, рост, длительность пребывания в стационаре и др. (количественные признаки, выраженные числом).

Различают так же факторные и результативные признаки в зависимости от характера влияния: какой признак на какой влияет (возраст – факторный признак, а рост - результативный).

Методами обработки медико – биолоических исследований являются методы расчета средних, относительных величин.

Одной из основных областей применения математической статистики в медицине является обоснование выводов, вытекающих из сравнения статистических показателей. Основным вопросом при этом является суждение о том, в какой мере обнаружения при исследовании разность между выборочными показателями может свидетельствовать о существенном, неслучайном различии генеральных совокупностей.

В статистике широкое применение нашла нулевая гипотеза Н₀. Так если одна выборка извлечена из генеральной совокупности с параметрами М(х) и σ_х, а другая – из совокупностей с параметрами М(Y) и σ_у, то нулевая гипотеза исходит из того, что М(х) – М(Y) = 0 и σ_х - σ_у = 0 (отсюда и название гипотезы – нулевая).

Противоположная нулевой – конкурирующая гипотеза Н₁ – исходит из предположения, что М(х) – М(Y) ≠ 0 и σ_х - σ_у ≠ 0.

Для проверки принятой гипотезы используют величины, функции распределения которых известны и сведены в специальные таблицы. Принимают три уровня значимости, или вероятности ошибки, допускаемой при проверке статистических гипотез:

5% -ный (вероятность ошибочной оценки Р = 0,05)

1% -ный (Р = 0,01)

0,1% ный (Р = 0,001).

В биологических исследованиях часто считают достаточным 5% -ный уровень значимости. При этом гипотезу Н₀ не отвергают, если вероятность ошибочности оценки относительно принятой гипотезы превышает 5%.

Если же эта вероятность меньше 5 %, то принятую гипотезу следует отвергнуть на взятом уровне. Ошибка при этом возможна не более, чем в 5 % случаев, т.е. она маловероятна. При более ответственных исследованиях уровень значимости может быть уменьшен до 1 % или даже 0,1 %.

В области биометрии применяются два вида статистических критериев.

Параметрические, построенные на основании параметров данной совокупности и представляющие функции этих параметров.

Непараметрические - представляющие собой функции, зависящие непосредственно от варианта данной совокупности с их частотами.

Дата добавления: 2014-10-22