Выявление взаимосвязей. Коэффициент корреляции

Критерии проверки статистических гипотез. Выявления достоверности различий.

Сопоставляя среднее значения контрольной и исследуемой групп, можно видеть, что они отличаются. Можно ли по этим данным сделать вывод о большей эффективности нового препарата? Для этого надо применить критерии Стьюдента.

Критерий Стьюдента позволяет найти вероятность случайного появления анализируемых выборок, и если оно меньше 0,05, то различия между выборками не случайны, т.е. лечение эффективно.

Коэффициент корреляции – параметр, характеризующий степень взаимосвязи между двумя выборками.

Если R = -1, то это строгая обратная линейная зависимость;

Если R = 0, то линейной зависимости между двумя выборками нет.

Для оценки степени взаимосвязи рассматривают R по абсолютной величине. Если 0,95 <R<1 – практически линейная зависимость;

0,8 <R<0,95 – сильная степень линейной связи между параметрами;

0,6 <R<0,8 – есть наличие линейной связи между параметрами;

Если R<0,4 – то считают, что линейную связь между параметрами выявить не удалось.

Регрессионный анализ использует коэффициент корреляции для прогнозирования процесса.

Пример: Параметрические критерии. Метод Стьюдента.

На двух группах лабораторных мышей – опытной(=9) и контрольной(=11) – изучали воздействие на организм нового препарата. После месячных испытаний масса тела животных, выраженная в граммах, варьировала следующим образом:

В опытной группе: 80,76,75,64,70,68,72,79,83.

В контрольной группе: 70,78,60,80,62,68,73,60,71,66,69.

Определить существенно ли действие на организм мышей препарата.

Решение:

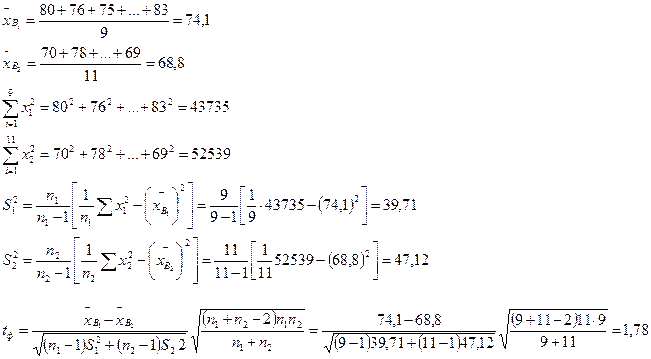
Табличные значения параметра t_st = 2,10 для k = n₁ + n₂ – 2 = 18 и (5% -ного уровня значимости). Т.к. 1,78 < 2,10 нулевая гипотеза остается в силе.

Дата добавления: 2014-10-22