Задачи на экстремум функции

Задачи на применение физического (механического) смысла производной.

Как известно, скорость ν прямолинейного движения материальной точки есть производная пути S = S(t) по времени t: v = ds/dt или v(t) = s^/(t)

Например: точка движется по прямой по закону S = t³ – 1, где S – путь (в см), а t – время (в с). Найти скорость движения в момент t = 3.

Решение: v(t) = s^/(t) = 3t², откуда, в частности, при t = 3, v(3) = 3·3² =3·9 = 27см/с.

Этот же способ решения задачи можно применить и медико-биологической задаче.

Пусть популяция некоторого вида бактерий в момент t насчитывает р(t) = 3000 + 100t² особей (при этом t измеряется в часах), то скорость роста данной популяции есть производная от р(t) = 3000 + 100t².

р^/(t) = (3000 + 100t²)^/ = 200t.

Скорость этой популяции увеличивается со временем. Если t = 5ч, то скорость роста составляет 200·5 = 1000 особей в час. Если t = 10ч, то скорость роста составляет 200·10 = 2000 особей в час.

Напомним следующее правило исследования функции f(x) на экстремум.

Чтобы найти точки экстремума данной функции f(x), следует:

1) Найти первую производную функция у = f(x) и, приравняв ее к нулю, вычислить действительные корни полученного уравнения f^/(x) = 0.

2) Найти вторую производную f^//(x).

3) Вычислить значение второй производной для каждого значения х, являющегося корнем первой производной.

Если при этом окажется, что f^//(x)≠0, где х₀ – взятый корень, то при х = х₀ функция f(x) имеет экстремум:

Максимум, если f^//(x)<0, и минимум, если f^//(x)>0.

Рассмотрим следующие задачи:

Задача №1: В питательную среду вносят популяцию из 1000 бактерий. Численность популяции возрастает по закону р(t) = 1000 +, где t

Выражается в часах. Найти максимальный размер этой популяции.

Решение. Имеем:

р^/(t) =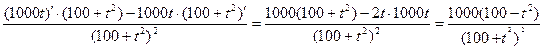

р^//(t) = (р^/(t))^/ =-2000t·(предлагаем вам самостоятельно найти данную производную и сравнить полученный результат).

Так как р^/(10) = 0 и р^// (10) <0, то максимальный размер популяции составляет р(10) = 1050 и достигается по происшествии 10 часов роста.

Задача №2. Реакция организма на введенное лекарство может выражаться повышением кровяного давления, уменьшением температуры тела, изменением пульса или других физиологических показателей. Степень реакции зависит от назначенной дозы лекарства. Предположим, что х обозначает дозу назначенного лекарства, а степень реакции у описывается функцией у = R(x) = x²(a – x), где а – некоторое положительное постоянное. При каком значении х реакция максимальна?

Решение. Имеем f^/ (x) = (x²(a – x))^/ = (х²)^/· (a – x) + x²(a – x)^\ =2х(a – x) – х² =

= 2 ax – 3x², f^// (x) = (2 a – 6x.

Так как х = 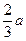- корень уравнения f^/ (x) = 0 и f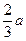^// () = -2 а <0, то х = 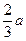- тот уровень дозы, который дает максимальную реакцию.

Задача №3.

Газовая смесь, необходимая для лабораторных исследований, состоит из окиси азота (NO) и кислорода (О₂). Требуется найти концентрацию О₂, при которой содержащаяся в смеси окись азота окисляется с наибольшей скоростью

Дата добавления: 2014-10-22