Методические указания к выполнению типового расчета

Задача 3.1. Найти матрицу X из уравнения

.

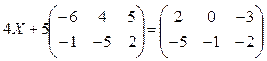Решение: Обозначим буквами матрицы данного уравнения и выразим искомую матрицу X:

4 X + 5 А = B

4 X = B - 5 A

X = 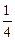(B - 5 A)

X = 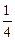(B + (-5) A).

Выполняя операции умножения матрицы на число и сложение матриц, получаем

X = ==

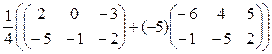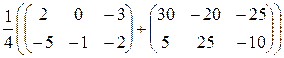= Þ X = .

Подставляя полученную матрицу X в исходное уравнение, получаем истинное тождество.

Ответ: X = .

Задача 3.2. Даны матрицы А = 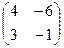, В = 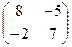. Вычислить AB – BA.

Решение: Размеры матриц 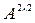и 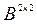согласованы, поэтому можно найти произведение матриц:

, тогда

.

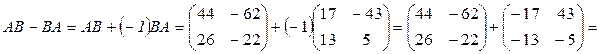
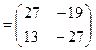Ответ: АВ - ВА = .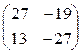

Задача 3.3. Найти матрицу D = A ^T× B × C, где

, , .

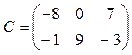Решение: Ввиду ассоциативности операции умножения матриц произведение 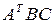можно вычислить, используя любой из двух способов: или . Вычислим произведение, используя 1-й способ (предлагаем вычислить определитель самостоятельно 2-м способом и сравнить полученные результаты). Заменяя в матрице А строки соответствующими столбцами получаем транспонированную матрицу A ^T:

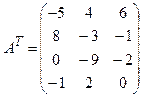
Поскольку размерности A ^T и B согласованы, можно вычислить

Размеры матриц A ^T B и С также согласованы, поэтому

.

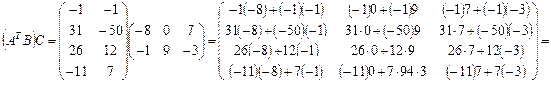
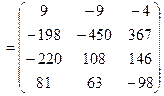Ответ: D = .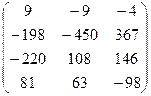

Задача 3.4. Решить уравнение .

Решение: Вычислим определитель 3-го порядка по правилу треугольников:

.

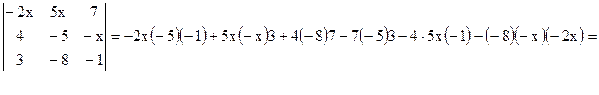
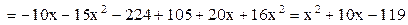Решаем уравнение:

Проверка: подставим полученные значения х₁ и х₂ в исходное уравнение:

,

вычислим определитель, разлагая по 3 столбцу:

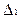= (-1) A₃₃ = (-1)(-1)³⁺³ M₃₃ = (-1)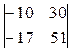= 0, (столбцы пропорциональны)

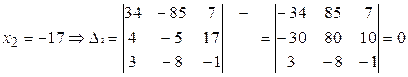(строки пропорциональны)

Ответ: x ₁ = 7, x ₂ = -17.

Задача 3.5. Используя формулу разложения по 3–му столбцу, вычислить определитель .

Решение: При разложении определителя по 3–му столбцу воспользуемся теоремой Лапласа. Пусть - искомый определитель

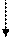
разлагая каждый из определителей по 3-й строке, получаем:

Ответ: Δ= - 250.

Задача 3.6. Используя метод приведения к треугольному виду, вычислить определитель .

Решение: Воспользуемся свойствами определителей для приведения определителя к треугольному виду. Используя свойства 9⁰, 4⁰, обратим в нули все элементы под главной диагональю

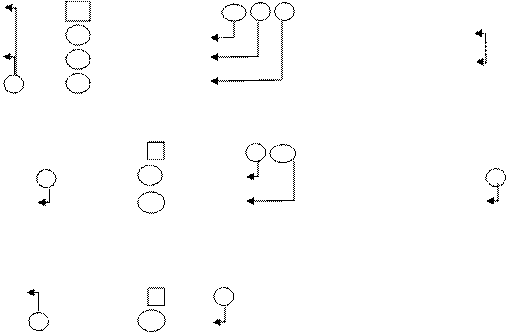
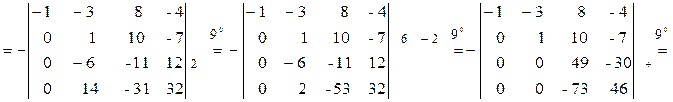
Ответ: 64.

Задача 3.7. Вычислить .

Решение: Вычислим определитель с помощью теоремы Лапласа, разложив его по элементам какой – либо строки (столбца). Преобразуем определитель матрицы так, чтобы во 2-м столбце все элементы, кроме одного, обратились в нуль. Раскладывая полученный определитель по элементам 2-го столбца, получим:

.

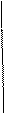
Упростим вид определителя и воспользуемся теоремой Лапласа

^.

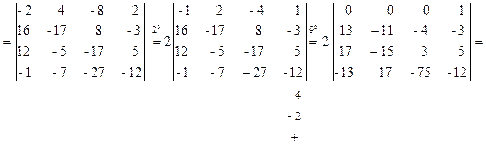
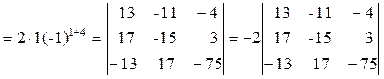Вновь упростим определитель и применим теорему Лапласа

.

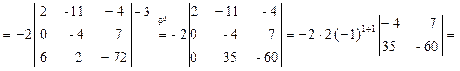
Ответ: .

Задача 3.8. Показать, что матрица 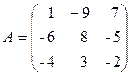обратима и найти А^-1. методом присоединенной матрицы.

Решение: Квадратная матрица А - обратима (имеет обратную А^-1) .

. Найдем обратную матрицу:

, где - присоединенная матрица.

Вычислим алгебраические дополнения элементов матрицы

.

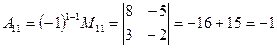
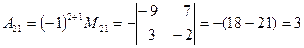
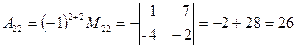
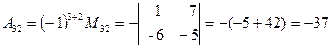
Правильность вычисления обратной матрицы можно проверить, используя определение обратной матрицы: .

Ответ: .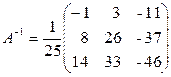

Задача 3.9. Решить матричное уравнение XA+B=C, если

, , .

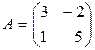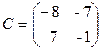Решение: Выразим из уравнения матрицу X

XA+B=C

Вычислим А^-1 для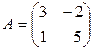

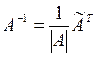, где .

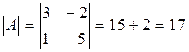Присоединенную матрицу второго порядка 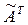для матрицы A находим по правилу: меняем местами элементы главной диагонали, а элементам побочной диагонали изменим знак. Получаем А^-1 = .

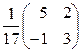Находим исходную матрицу: .

Используя свойство 7° операций над матрицами, получаем

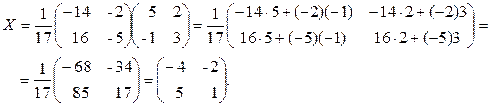
Правильность вычисления матрицы можно проверить подстановкой в исходное уравнение.

Ответ: Х = .

Задача 3.10. С помощью элементарных преобразований над строками найти матрицу, обратную данной A = .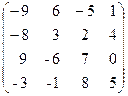

Решение: С помощью элементарных преобразований над строками прямоугольную матрицу 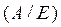приведем к виду

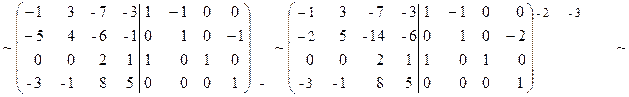
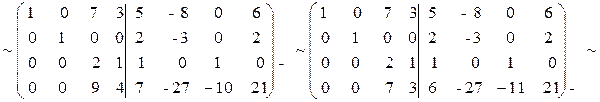
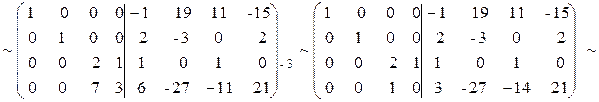
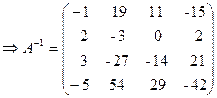
Правильность вычисления А^-1 можно проверить, используя определение обратной матрицы .

Ответ: .

ЛИТЕРАТУРА

Дата добавления: 2014-10-22