Задачи для самостоятельного решения. Задание 1. Решить задачи методом потенциалов

Задание 1. Решить задачи методом потенциалов. Сравнить найденное решение с решением, полученным в MS Excel.

1. Фирма, обслуживающая туристов прибывающих на отдых, должна разместить их в четырех отелях: «Морской», «Солнечный», «Слава» и «Уютный», в которых забронировано соответственно 5, 15, 15 и 10 мест. По железной дороге прибывают 15 туристов, очередным рейсом в аэропорт прилетают 25, а на морской вокзал прибудут на теплоходе 5 чел. Транспортные расходы (ден. ед. на 1 чел.) при перевозке из пунктов прибытия в отели приведены в табл. 3.12.

Таблица 3.12.

Пункт прибытия	Транспортные расходы при перевозке в отели, ден. ед.
«Морской»	«Солнечный»	«Слава»	«Уютный»
Железнодорожный вокзал
Аэропорт
Морской вокзал

В условиях жесткой конкуренции фирма должна минимизировать свои расходы, значительную часть которых составляет именно расходы на транспорт. Требуется определить такой план перевозки туристов из пункта прибытия в отели, при котором суммарные транспортные расходы будут минимальны и все туристы будут размещены в отелях.

2. Четыре овощехранилища каждый день обеспечивают картофелем три магазина. Магазины подали заявки соответственно, на 17, 12 и 32 т; овощехранилища имеют соответственно 20, 20, 15 и 25 т. Транспортные тарифы за перевозку картофеля от овощехранилища до магазина (ден. ед. за 1 т) указаны в табл. 3.13.

Таблица 3.13

Овощехранилище	Расход на перевозку до магазина, ден. ед. за 1 т

Составьте план перевозок, минимизирующий суммарные транспортные расходы.

3. Имеются два склада готовой продукции: А₁ и А₂ с запасами однородного груза 200 и 300 т. Этот груз необходимо доставить трем потребителям: В₁, В₂, В₃ в количестве 100, 150, 250 т соответственно. Стоимость перевозки 1 т груза из склада А₁, потребителям В₁, В₂ и В₃ равна 5, 3, 6 ден. ед., а из склада А₂ тем же потребителям - 3, 4, 2 ден. ед. соответственно. Определить план перевозок, минимизирующий суммарные транспортные расходы.

4. Заводы 1, 2, 3 производят однородную продукцию в количестве соответственно 500, 400 и 510 ед. Себестоимость производства 1 ед. продукции на заводе 1 составляет 25 ден. ед., на заводе 2 - 20 ден. ед., на заводе 3 - 23 ден. ед. Продукция отправляется в пункты А, В, С, потребности которых равны 310, 390 и 450 ед. Минимизировать издержки, если стоимость перевозок 1 ед. продукции задана матрицей

.

5. Имеются три специализированные мастерские - I, II, III по ремонту двигателей. Их производственные мощности равны соответственно 100, 700, 980 ремонтов в год. В пяти районах, обслуживаемых этими мастерскими, потребность в ремонте равна соответственно 90, 180, 150, 120, 80 двигателей в год. Затраты на перевозку одного двигателя из районов к мастерским приведены в табл. 3.14. Спланируйте количество ремонтов каждой мастерской для каждого из районов, минимизирующее суммарные транспортные расходы.

Таблица 3.14

Район	Расход на перевозку к мастерским, ден. ед.
I	II	III
	4,5	3,7	8,3
	2,1	4,3	2,4
	7,5	7,1	4,2
	5,3	1,2	6,2
	4,1	6,7	3,1

6. Имеются 3 элеватора (I, II, III), в которых сосредоточено соответственно 1000, 2000 и 1600 т зерна. Зерно необходимо перевезти на два хлебозавода в количестве 4200 и 1200 т каждому. Расстояние от элеватора до хлебозавода (км) указано в табл. 3.15. Затраты на перевозку 1 т продукта на 1 км составляют 25 ден. ед. Спланируйте перевозки зерна из условия минимизации транспортных расходов.

Таблица 3.15

Хлебозавод	Расстояние от элеватора до завода, км
I	II	III

7. На строительство четырех объектов кирпич поступает с трех (I, II, III) заводов. Заводы имеют на складах соответственно 50, 100 и 50 тыс. шт. кирпича. Объекты требуют соответственно 50, 70, 40, 40 тыс. шт. кирпича. Тарифы (ден. ед./ тыс. шт.) приведены в табл. 3.16.

Таблица 3.16

Завод	Тариф, ден. ед./тыс. шт.
I
II
III

Составьте план перевозок, минимизирующий суммарные транспортные расходы.

8. Для полива трех участков сада (I, II, III), на которых растут сливы, яблони и груши, служат три колодца. Колодцы могут дать соответственно 180, 90 и 40 ведер воды. Участки сада требуют для полива соответственно 100, 120 и 90 ведер воды. Расстояние (в метрах) от колодца до участка сада указано в табл. 3.17. Как лучше организовать полив?

Таблица 3.17

Колодец	Расстояние от колодца до участка, км
I	II	III

9. Для строительства четырех объектов используется кирпич, изготовляемый на трех заводах. Ежедневно каждый завод может изготовлять 100, 150 и 50 ед. кирпича. Ежедневные потребности в кирпиче на каждом строящемся объекте соответственно равны 75, 80, 60 и 85 ед. Известны также тарифы перевозок 1 ед. кирпича с каждого завода к каждому строящемуся объекту:

.

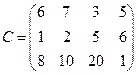Составить такой план перевозок кирпича к строящимся объектам, при котором общая стоимость перевозок является минимальной.

10. На трех хлебокомбинатах ежедневно производится 110, 190 и 90 т муки. Эта мука потребляется четырьмя хлебозаводами, ежедневные потребности которых равны соответственно 80, 60, 170 и 80 т. Тарифы перевозок 1 т муки с хлебокомбинатов к каждому из хлебозаводов задаются матрицей

.

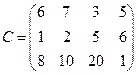Составить такой план доставки муки, при котором общая стоимость перевозок является минимальной.

11. В трех хранилищах горючего ежедневно хранится 175, 125 и 140 т бензина. Этот бензин ежедневно получают четыре заправочные станции в количествах, равных соответственно 180, 110, 60 и 40 т. Стоимость перевозок 1 т бензина с хранилищ к заправочным станциям задаются матрицей

.

Составить план поставок бензина заправочным станциям с минимальной стоимостью.

12. Три молочные фермы (I, II, III) с суточным производством 40, 25 и 35 тыс. л молока снабжают четыре молокозавода, спрос которых: 15, 40, 30 и 15 тыс. л молока в сутки. Молоко доставляется на заводы одинаковыми по вместимости молоковозами. Стоимость перевоза молока на расстояние 1 км составляет 3 ден. ед. Расстояние от фермы до молокозавода приведено в табл. 3.18.

Таблица 3.18

Ферма	Расстояние от фермы до молокозавода, км
I
II
III

Найти оптимальный план поставки молока с ферм на молокозаводы с минимальными транспортными издержками. Рассчитать стоимость доставки молока от каждой фермы до молокозавода.

13. Четыре бензохранилища (I, II, III, IV) с суточным объемом хранения 60, 40, 100 и 50 тыс. т авиационного бензина снабжают пять аэропортов, спрос на бензин которых составляет 30, 80, 65, 35 и 40 тыс. т бензина в сутки. Бензин транспортируется в аэропорты одинаковыми по вместимости бензозаправщиками. Стоимость провоза бензина бензозаправщиком на расстояние 1 км составляет 7 ден. ед. Расстояние от бензохранилища до аэропорта дано в табл. 3.19.

Найти оптимальный план поставки бензина с минимальными транспортными издержками. Рассчитайте стоимость доставки бензина от каждого аэропорта до хранилища.

Таблица 3.19

Бензохранилище	Расстояние от бензохранилища до аэропорта, км
I
II
III
IV

14. Торговая фирма «Весна и осень» включает четыре предприятия (I, II, III, IV) и шесть складов в различных регионах страны. Каждый месяц предприятия фирмы производят 100, 15, 90 и 55 ед. продукции. Вся производимая продукция направляется на склады, вместимость которых соответственно 30, 40, 55, 80, 45 и 10 ед. продукции. Денежные издержки на транспортировку продукции от предприятий до складов (ден. ед.) даны в табл. 3.20.

Таблица 3.20

Предприятие	Расход на транспортировку до склада, ден. ед.
I
II
III
IV

Распределите план перевозок исходя из условия минимизации ежемесячных расходов на транспортировку.

15. Деревообрабатывающий комбинат имеет три цеха: А, В, С и четыре склада. Цеха и склады находятся на разных территориях. Цех А производит 40 тыс. м³ материала, цех В – 30 тыс. м³; цех С – 20 тыс. м³ материала. Пропускная способность складов за то же время следующая: склад 1 – 30 тыс. м³ материала, склад 2 – 25 тыс. м³, склад 3 – 15 тыс. м³ и склад 4 – 20 тыс. м³ материала. Стоимость перевозки 1 м³ материала из цеха А на склады 1, 2, 3, 4 соответственно: 10, 20, 60, 40 ден. ед., из цеха В - соответственно 30, 10, 30, 20, а из цеха С - соответственно 50, 70, 50, 10 ден. ед.

Составьте план перевозки изделий, при котором расходы на перевозку материала были бы наименьшими.

16. Для строительства четырех участков дорожной магистрали необходимо завозить песок. Песок может быть поставлен из трех карьеров (I, II, III). Перевозка песка от карьера до участка осуществляется грузовиками одинаковой грузоподъемности. Расстояния от карьеров до участков и количество песка в каждом карьере приведены в табл. 3.21. Потребность в песке на каждом участке дороги: 1 – 15 тыс. т, 2 – 15 тыс. т, 3 – 40 тыс. т, 4 – 30 тыс. т.

Таблица 3.21

Карьер	Расстояние от карьера до участка, км	Количество песка в карьере, тыс. т
I
II
III

Составьте план перевозок, минимизирующий общий пробег грузовиков.

17. Имеются четыре овощехранилища (I, II, III, IV), расположенные в разных районах города, в которых сосредоточено соответственно 10, 20, 35 и 45 т овощей. Овощи необходимо перевезти четырем потребителям в количестве соответственно 25, 30, 40 и 15 т. Расстояния от хранилищ до потребителей (км) даны в табл. 3.22. Затраты на перевозку 1 т овощей на 1 км постоянны и равны 20 руб.

Таблица 3.22

Хранилище	Расстояние от хранилища до потребителя, км
I
II
III
IV

Определить план перевозок продукта от хранилищ до потребителей из условия минимизации транспортных расходов.

18. Четыре растворных узла (I, II, III, IV) поставляют раствор четырем строительным фирмам. Для перевозки раствора используются однотипные автомашины. Объем производства растворных узлов в день равен 30, 20, 40, 50 т. Потребности строительных фирм в день: 35, 20, 55, 30 т. Расстояния в километрах от растворных узлов до строительных объектов указаны в табл. 3.23.

Таблица 3.23

Растворный узел	Расстояние от узла до строительной фирмы, км
I
II
III
IV

Определить, в каком объеме, из каких растворных узлов и куда должен доставляться раствор, чтобы транспортные издержки по его доставке автотранспортом были минимальными.

19. Требуется спланировать перевозку строительного материала с трех заводов на четыре строительные площадки с минимальными затратами, используя железнодорожную сеть. В течение каждого квартала на четырех площадках требуется соответственно 5,10, 20,15 вагонов строительных материалов. Возможности трех заводов равны соответственно 10, 15 и 25 вагонов в квартал. Стоимость перевозки одного вагона (ден. ед.) приведена в табл. 3.24.

Таблица 3.24

Заводы	Строительные площадки

20. Организация получила заказы на три вида выпускаемой ею продукции (бокалы, чашки и вазы), которые необходимо изготовить в течение недели. Размеры заказов: бокалы - 4000 шт., чашки - 2400 шт., вазы - 1000 шт. Участок по изготовлению имеет три станка. Производственные мощности 2-го и 3-го станков на эту неделю составят по 3000 шт., а 1-го станка - 2000 шт. Единичные затраты (ден. ед.) по каждому виду продукции различны в зависимости от используемого станка и приведены в табл. 3.25.

Таблица 3.25

Станок	Бокалы	Чашки	Вазы
	1,2	1,3	1,1
	1,4	1,2	1,5
	1,1	1,0	1,3

Найти план производства для заказанных видов продукции с наименьшей стоимостью.

Задание 2. Решить задачи при условии целочисленности компонент в оптимальном плане методом ветвей и границ. Сравнить найденное решение с решением, найденным в MS Excel.

1. ;	2. ;
3. 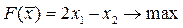;	4. ;
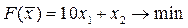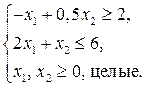
5. ;	6. ;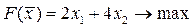
7. ;	8. ;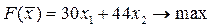
9. ;	10. ;
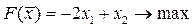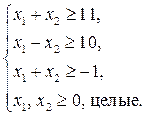
11. ;	12. ;
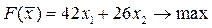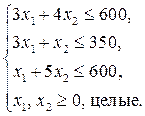
13. ;	14. ;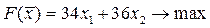
15. ;	16. ;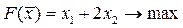
17. 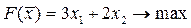;	18. ;
19. ;	20. ;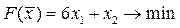

Дата добавления: 2014-10-22