
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Выпуклое программирование
|
|
|
|
Рассмотрим задачу выпуклого программирования:
 (4.5)
(4.5)
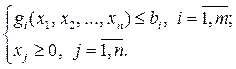 (4.6)
(4.6)
где  является выпуклой (вогнутой) функцией; функции
является выпуклой (вогнутой) функцией; функции  - выпуклыми.
- выпуклыми.
Метод решения задачи выпуклого программирования опирается на теорему Куна-Таккера.
Функция  , заданная на выпуклом множестве X, называется выпуклой, если для любых двух точек Х1 и Х2 из множества X и любого
, заданная на выпуклом множестве X, называется выпуклой, если для любых двух точек Х1 и Х2 из множества X и любого  выполняется соотношение
выполняется соотношение
 .
.
Функция  , заданная на выпуклом X, называется вогнутой, если для любых двух точек Х1 и Х2 из множества X и любого
, заданная на выпуклом X, называется вогнутой, если для любых двух точек Х1 и Х2 из множества X и любого  выполняется соотношение
выполняется соотношение
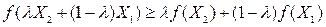 .
.
Множество допустимых решений задачи (4.5)-(4.6) удовлетворяет условию регулярности, если существует, по крайней мере, одна точка Xk, принадлежащая области допустимых решений, такая, что  .
.
Функцией Лагранжа задачи выпуклого программирования (4.5), (4.6) называется функция
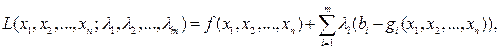
где  - множители Лагранжа.
- множители Лагранжа.
Теорема Куна-Таккера. Для задачи выпуклого программирования (4.5), (4.6), множество допустимых решений которой обладает свойством регулярности, 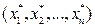 является оптимальным решением тогда и только тогда, когда существует такой вектор
является оптимальным решением тогда и только тогда, когда существует такой вектор 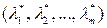 , где
, где 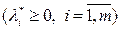 , что точка
, что точка 
 является седловой точкой функции Лагранжа.
является седловой точкой функции Лагранжа.
Если функции  и
и 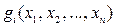 непрерывно дифференцируемы, то теорема Куна-Таккера может быть дополнена аналитическими выражениями, определяющими необходимые и достаточные условия того, чтобы точка
непрерывно дифференцируемы, то теорема Куна-Таккера может быть дополнена аналитическими выражениями, определяющими необходимые и достаточные условия того, чтобы точка 
 была седловой точкой функции Лагранжа, а
была седловой точкой функции Лагранжа, а 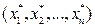 - оптимальным решением задачи выпуклого программирования. Эти условия имеют следующий вид:
- оптимальным решением задачи выпуклого программирования. Эти условия имеют следующий вид:


 (4.7)5
(4.7)5



 (4.7)6
(4.7)6

где 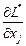 и
и  - значения соответствующих частных производных функции Лагранжа, вычисленных в седловой точке.
- значения соответствующих частных производных функции Лагранжа, вычисленных в седловой точке.
Алгоритм решения задач выпуклого программирования
Шаг 1. Составляют функцию Лагранжа.
Шаг 2. Записывают необходимые и достаточные условия существования седловой точки для функции Лагранжа (4.7)56.
Шаг 3. Находят решение системы (4.7)56 и из него получают оптимальное решение задачи выпуклого программирования.
Пример 2. Найти оптимальное решение следующей задачи выпуклого программирования:
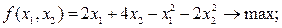

Решение. Функция f (xl, x2) является вогнутой, поскольку представляет собой сумму линейной функции 2 х1 +4 x2 (которую можно рассматривать как вогнутую) и квадратичной формы  , которая является отрицательно-определенной и, следовательно, также вогнутой. Система ограничений задачи включает только линейные неравенства, поэтому область допустимых решений выпуклая. Следовательно, можно воспользоваться теоремой Куна-Таккера.
, которая является отрицательно-определенной и, следовательно, также вогнутой. Система ограничений задачи включает только линейные неравенства, поэтому область допустимых решений выпуклая. Следовательно, можно воспользоваться теоремой Куна-Таккера.
Составим функцию Лагранжа

и запишем, используя (4.7)56, необходимые и достаточные условия существования седловой точки построенной функции:

 (4.8)7
(4.8)7





 (4.9)8
(4.9)8

Систему линейных неравенств (4.8)7 перепишем следующим образом:


 (4.10)9
(4.10)9


Введем теперь дополнительные неотрицательные переменные v1, v2, w1 и w2, обращающие неравенства (4.10)9 в равенства:


 (4.11)10
(4.11)10


С учетом дополнительных переменных соотношения в системе (4.9)8 можно записать в виде:
 (4.12)11
(4.12)11
Для нахождения базисного решения системы линейных уравнений (4.11)10 с учетом выполнения равенств (4.12)11 воспользуемся методом искусственного базиса. В первое и второе уравнения системы (4.11)10 введем дополнительные неотрицательные переменные z1 и z2 соответственно и рассмотрим задачу линейного программирования:






Чтобы решить эту задачу, сначала находим ее допустимое базисное решение (таблица 4.1).
Из таблицы 4.1 получаем:

Таблица 4.1
| ci | БП | 0 | 0 | 0 | - M | - M | bi | |||||
| x1 | x2 | l1 | l2 | v1 | v2 | w1 | w2 | z1 | z2 | |||
| - М | z1 | -1 | ||||||||||
| - М | z2 | -1 | -1 | |||||||||
| w1 | ||||||||||||
| w2 | -1 | |||||||||||
| Dj | -2 | -4 | -3 | -1 | -1 | -1 | -6 | |||||
| - М | z1 | -1 | ||||||||||
| x2 | 1/2 | -1/4 | -1/4 | |||||||||
| w1 | -1 | 1/2 | 1/2 | |||||||||
| w2 | 1/2 | -1/4 | -1/4 | |||||||||
| Dj | -2 | -1 | -2 | -1 | -2 | |||||||
| x1 | 1/2 | -1/2 | ||||||||||
| x2 | -1/2 | -1/2 | ||||||||||
| w1 | -3/2 | -1/2 | 1/2 | 1/2 | ||||||||
| w2 | -1/2 | -3/4 | -1/4 | |||||||||
| Dj |
Так как  , заключаем, что точка (
, заключаем, что точка ( ) является седловой точкой функции Лагранжа для исходной задачи. Следовательно,
) является седловой точкой функции Лагранжа для исходной задачи. Следовательно,  - оптимальное решение исходной задачи, fmax = 3.
- оптимальное решение исходной задачи, fmax = 3.
|
|
|
|
|
Дата добавления: 2014-10-22; Просмотров: 1215; Нарушение авторских прав?; Мы поможем в написании вашей работы!