Закон больших чисел

В широком смысле под законом больших чисел понимают общий принцип, согласно которому при большом числе случайных величин их среднее перестает быть случайным и может быть предсказано с большой степенью определенности. В узком смысле закон больших чисел – это ряд теорем, в каждой из которых устанавливается факт приближения средних результатов большого числа испытаний к определенным постоянным.

В дальнейшем будет обсуждаться случайная величина – среднее арифметическое случайных величин, которую для краткости обозначим символом 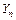. Заметим, что математическое ожидание среднего арифметического 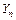равно среднему арифметическому математических ожиданий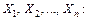

.

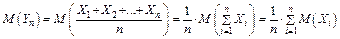Аналогично дисперсия среднего арифметического 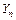в случае независимости случайных величин 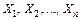выражается через их дисперсии по формуле:

.

Теорема 8.1 (Чебышева): Если дисперсии 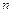попарно независимых случайных величин 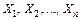ограничены одной и той же постоянной то при 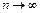среднее арифметическое этих случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий:

Замечание: 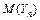– постоянная, то есть неслучайная величина, поэтому смысл теоремы Чебышева состоит в том, что среднее арифметическое 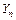случайных величин 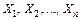при 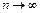перестает быть случайной величиной и становится практически достоверной, сколь угодно мало отличаясь от математического ожидания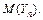

Следствие: Для независимых случайных величин 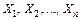с одинаковыми математическими ожиданиями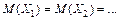 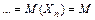и дисперсиями, ограниченными одной и той же постоянной , их среднее арифметическое сходится по вероятности к :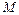

Теорема 8.2 (Бернулли): Если в каждом из 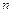независимых повторных испытаний событие может произойти с одной и той же вероятностью 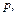то статистическая вероятность этого события при неограниченном увеличении числа опытов сходится по вероятности к вероятности этого события в единичном испытании.

Замечание: Эта теорема – частный случай теоремы Чебышева – исторически была первой формой закона больших чисел, она дает теоретическое обоснование замены классической вероятности события на статистическую при большом числе опытов. Например, в качестве неизвестной вероятности рождения мальчика можно принять приближенную относительную частоту этого события 0,515.

Теорема 8.3 (Хинчина): При достаточно большом числе независимых испытаний среднее арифметическое значений случайной величины, наблюдаемых в ходе опытов, сходится по вероятности к ее математическому ожиданию, если оно существует.

Все рассмотренные выше формы закона больших чисел относятся к независимым случайным величинам. На зависимые случайные величины закон больших чисел распространил А. Марков.

Теорема 8.4 (Маркова): Если при неограниченном увеличении числа испытаний 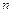для зависимых случайных величин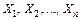 то среднее арифметическое этих случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий:.

Дата добавления: 2014-10-23