Логарифмическая амплитудно-фазочастотная характеристика

Амплитудно-фазочастотные характеристики колебательного звена

Переходная функция

. (4.81)

Корни характеристического уравнения колебательно звена (0< e <1) равны:

p ₁=0, p _2,3 =. (4.82)

Подставляя корни в формулу обратного преобразования Лапласа (3.9), получим:

(4.83)

Переходная характеристика колебательного звена представлена в таблице 4.10.

4.6.3.1 Амплитуднофазочастотная характеристика (АФЧХ):

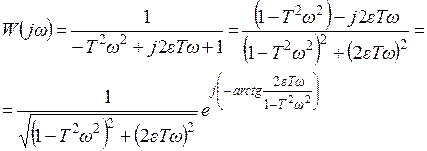. (4.84)

4.6.3.2 Амплитудночастотная характеристика (АЧХ):

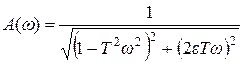. (4.85)

4.6.3.3 Фазочастотная характеристика (ФЧХ):

. (4.86)

4.6.3.4 Вещественная частотная характеристика (ВЧХ):

. (4.87)

4.6.3.5 Мнимая частотная характеристика (МЧХ):

. (4.88)

Амплитудно-фазочастотные характеристики представлены в таблице 4.10.

4.6.4.1 Логарифмическая амплитудночастотная характеристика (ЛАЧХ):

(4.81)

. (4.89)

ЛАЧХ колебательного звена можно построить аналитически по формуле и аппроксимировано.

Для построения аппроксимированным способом проанализируем поведение характеристики в двух областях частот:

- wT <<1 (ω <<1/T), тогда L (w)» – 20 lg 1=0.

- wT >>1 (ω >>1/T), тогда L (w)» – 40 lg wT – прямая линия с наклоном минус 40 дБна декаду, проходящая через частоту с координатами w =1/T L(ω)=0;

- w =1/T, L (w)= – 20 lg 2 e.

Алгоритм построения аппроксимированным способом аналогичен алгоритму для апериодического звена, но после частоты сопряжения наклон характеристики равен минус 40 дБ на декаду.

Максимальная погрешность построения будет при частоте сопряжения w_s =1/T. Значения ЛАЧХ при этой частоте для различных значений коэффициента затухания e показаны в таблице 4.9.

Из таблицы видно, что при e =0.05 будет значительное отклонение аппроксимированной ЛАЧХ от теоретической.

Таблица 4.9 – Значения ЛАЧХ при частоте сопряжения

e	0.5	0.05
L (w), дБ			-6

Таким образом, ЛАЧХ колебательного звена можно построить с помощью двух прямых, пересекаемых в точке с координатами w =1/T ,L(ω)=0, только при условии ε>0. В противном случае нужно строить:

- аналитически по формуле (4.90);

- используя типовые логарифмические графики, приведенные в литературе.

4.6.4.2 Логарифмическая фазочастотная характеристика (ЛФЧХ):

. (4.90)

Фаза изменяется от 0 до минус 180⁰ при изменении частоты от 0 до ∞ _. При частоте сопряжения (ω_s=1/T) фаза колебательного звена равна минус 90⁰ [.

Построение ЛФЧХ колебательного звена осуществляется только аналитически, или с помощью специальных графиков, приведенной в литературе.

Логарифмические амплитудно-фазочастотные характеристики представлены в таблице 4.12.

На рисунке 4.12 представлены временные характеристики входного и выходного синусоидальных напряжений при разных частотах. Из графиков видно, что в области малых частот (меньше частоты среза) синусоидальный входной сигнал практически не изменяется. В области высоких частот сигнал значительно ослабляется. При частоте сопряжения амплитуда резко повышается, то есть возникает явление резонанса.

Фазовый сдвиг выходного сигнала относительно входного изменяется от 0 до минус 180 градусов (рисунок 4.12).

Таблица 4.12 – Колебательное звено (апериодическое второго порядка)

Дифференциальное уравнение	Передаточная функция	Переходная характеристика
Уравнение	График
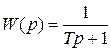
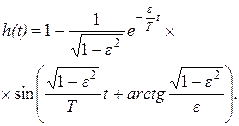
АФЧХ	ЛАФЧХ
Уравнение	График	Уравнение	График

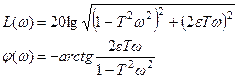
Дата добавления: 2014-10-23