Частотные методы

Связь между переходной и вещественной характеристиками доказана в [1,2,3] и выражается формулой:

(7.6)

. (7.8)

Из данного уравнения можно видеть, что переходной процесс можно построить при известной вещественной частотной характеристике.

ВЫВОД: оценить качество переходного процесса можно по форме вещественной частотной характеристики замкнутой системы.

Введем параметры, от которых зависят показатели качества переходной характеристики (Рисунок 7.2):

1. Значение ВЧХ при ω =0 P(0).

2. Значение ВЧХ при ω→∞ P(∞).

3. Максимальное значения ВЧХ.

4. Частота положительности - частота, при которой ВЧХ первый раз становится равной нулю.

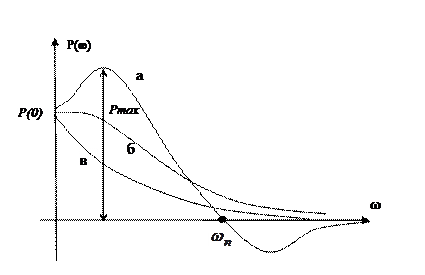
Рисунок 7.2

Основные характеристики переходной характеристики можно оценить следующим образом:

1) по значению ВЧХ при частоте, равной нулю P(0), определяется установившееся значение выходного сигнала h_уст;

2) по значению ВЧХ в области высоких частот P(ω→¥) определяется начальное значение выходного сигнала h (0);

3) значение перерегулирования s_m оценивается по формуле:

(7.9)

;

4) перерегулирование при невозрастающей ВЧХ (P ³0, 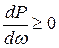) не превышает 18% (кривая б на риснке 7.2);

5) переходной процесс будет происходить без перерегулирования, если ВЧХ будет монотонно убывающей () – кривая в на рисунке 7.2.

6) время переходного процесса для трапецеидальной ВЧХ находится в интервале: 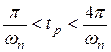. Время регулирования тем больше, чем больше коэффициент (кси)(см. рисунок 7.3);

4) время регулирования оценивается по частоте положительности w _п, более точно по номограммам Солодовникова (необходимо знать частоту среза w _c??????);

5) чем круче идет ВЧХ в области частоты положительности, тем больше время регулирования и колебательность.

6) при изменении масштаба по оси ординат ВЧХ, также изменяется масштаб по оси ординат переходной характеристики (ПХ):

; (7.10)

7) при увеличении масштаба по частоте w в «n» раз, во столько же раз уменьшится масштаб по оси времени ПХ:

(7.11)

;

8) любая ВЧХ может быть представлена алгебраической суммой трапециидальных ВЧХ;

9) переходные характеристики для ВЧХ, отличающихся в области высоких частот (больше частоты положительности), будут отличаться только в начальные моменты времени, а показатели качества будут примерно одинаковыми;

10) Переходные характеристики для ВЧХ, отличающихся в области низких частот, будут существенно отличаться друг от друга и соответственно иметь разные показатели качества.

Расчет и построение вещественной частотной характеристики осуществляется несколькими способами.

А. Аналитический:

пусть

(7.12)

,

где H(w) – АЧХ разомкнутой системы;

Q(w) – ФЧХ разомкнутой системы.

Проведя тригонометрические преобразования уравнения (7.12) ВЧХ замкнутой системы можно представить следующим образом:

(7.13)

По формуле (7.13) построена номограмма [1] для определения ВЧХ замкнутой системы с единичной обратной связью по ЛАФЧХ разомкнутой системы:

L_р=20lgH(w), Q(w). (7.14)

Алгоритм построения ЛАФЧХ системы с неединичной обратной связь:

1. строятся L_р(w), j_р(w) как сумма логарифмических характеристик прямого (L_п, j_п) и обратного каналов (L₀, j₀),

2. для некоторой частоты откладываются по осям номограммы эти значения, ищем точку с этими координатами, определяем ближайшее значение P и Q,

3. определяем. Значения P₀ и Q₀ можно определить по номограммам в [1] в зависимости от значений L₀ и j₀;

4. повторяем п. 2-3 для других частот.

Б) графоаналитический:

1. строятся логарифмические характеристики замкнутой системы,

2. для ряда частот определяются значения L_з и j_з,

3. рассчитывается и строится вещественная частотная характеристика по формуле:

	(7.15)

,

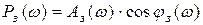где

(7.16)

.

В) Построение переходной характеристики по ВЧХ методом трапеций (по h-таблицам)

Любую ВЧХ можно разбить на алгебраическую сумму нескольких трапеций. Поэтому можно вычислить переходной процесс для граничного случая – единичные трапецеидальные ВЧХ, имеющие единичную высоту и частоту w ₀=1 и параметр (хи) c=0…1. Путем вычисления обратного преобразования Фурье были получены h-таблицы [1].

Алгоритм построения переходной характеристики по ВЧХ:

1) строится ВЧХ замкнутой системы;

2) ВЧХ разбивается на трапеции (для правильного разбивания на трапеции необходимо соблюдать обязательные условия (рисунок 7.4):

– трапеции, у которых верхнее основание меньше нижнего, принимаются отрицательными,

- сумма высот трапеций должна равна P (0),

- все трапеции должны начинаться с частоты равной 0.

3) вычисляются необходимые параметры для каждой трапеции (h_i, w_{0 i}, w_{d i}, c_i);

4) по h-таблицам определяются табличные значения переходных характеристик для единичных трапеций;

5) на основании свойств ВЧХ вычисляются истинные значения переходных характеристик как: h_истi=h_табл.i*h_i; t_ист.i=t_табл.i/w_{0 i}.

6) полученные таким образом переходные характеристики складываются с учетом знака;

7) проверяется установившееся значение переходной характеристики, которое должно быть равным P (0)

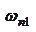
7.4 Оценка переходной характеристики с помощью ЛАЧХ замкнутой и разомкнутой системы

Оценка реакции системы при ступенчатом входном воздействии сопряжена, как правило, с громоздкими вычислениями. Поэтому очень важно уметь оценивать качество переходного процесса по виду логарифмических амплитудно-фазочастотных характеристик, которые строятся чаще всего асимптотическим (аппроксимированным) способом [1,2,3].

По виду логарифмической амплитудной частотной характеристики системы можно оценить основные параметры качества переходного процесса.

Для оценки показателей качества САУ используется ЛАЧХ или разомкнутой, или замкнутой системы.

Логарифмическая амплитудно-частотную характеристика разомкнутой системы условно разбивается на три диапазона частот:

- область высоких частот,

- область низких частот,

- область средних частот.

Поведение ЛАЧХ в области высоких частот характеризует начало переходного процесса и начальное значение выходной координаты:

1) если в этой области ЛАЧХ имеет отрицательный наклон, то значение выходной координаты в начальный момент времени равно нулю;

2) если ЛАЧХ имеет нулевой наклон, то выходная координата при t = 0 отлична от нуля и определяется значением предела передаточной функции замкнутой системы при переменной p стремящейся к ¥;

3) если ЛАЧХ имеет положительный наклон, то выходная координата при t = 0 стремится к бесконечности. Такие САУ имеют большую чувствительность к помехам, поэтому при проектировании следует избегать такого рода характеристик.

Поведение ЛАЧХ в области низких частот характеризует окончание переходного процесса, установившееся значение выходной координаты и точность системы;

1) если в этой области ЛАЧХ имеет отрицательный наклон, то проектируемая система астатическая, т.е. ошибка регулирования равна нулю;

2) если ЛАЧХ имеет нулевой наклон, то замкнутая система статическая, т.е. ошибка регулирования отлична от нуля. Значение выходной координаты можно определить по уравнению передаточной функции замкнутой САУ, в которой вместо оператора Лапласа «р» необходимо поставить нуль;

3) если ЛАЧХ имеет положительный наклон, то установившееся значение выходной координаты после окончания переходного процесса будет равно нулю.

Поведение ЛАЧХ в области средних частот (область в районе частоты среза системы) характеризует протекание переходного процесса:

1) если через частоту среза ЛАЧХ проходит с наклоном – 60 дБ/дек, то замкнутая система будет неустойчивой, и необходимо рассмотреть вопросы устойчивости и коррекции;

2) если через частоту среза ЛАЧХ проходит с наклоном – 40 дБ/дек, то замкнутая система будет иметь минимальные запасы устойчивости по амплитуде и фазе, и, следовательно, большое перерегулирование и колебательность. САУ также может быть и неустойчивой;

3) если через частоту среза ЛАЧХ проходит с наклоном – 20 дБ/дек, то замкнутая система будет иметь достаточные запасы устойчивости по амплитуде и фазе, и, следовательно, перерегулирование и колебательность будет не столь большим. Чем больше диапазон частот в районе частоты среза с наклоном – 20 дБ/дек, тем большими запасами устойчивости обладает замкнутая система, По частоте среза оценивается время регулирования:

(7.7)

.

Если имеется ЛАЧХ замкнутой системы, оценка качества переходного процесса производится следующим образом.

1. Установившееся значение выходной координаты h_¥ определяется ординатой ЛАЧХ при нулевой частоте.

2. Переходной процесс протекает без перерегулирования, если ординаты ЛАЧХ на всех частотах не превышают ординаты ЛАЧХ при нулевой частоте.

3. Максимум ЛАЧХ на любой частоте, кроме нулевой, свидетельствует о том, что процесс протекает с перерегулированием. Максимальное превышение выходной координаты приблизительно равно входному сигналу, умноженному на максимальное значение коэффициента усиления амплитуды при этой частоте.

4. Переходной процесс до достижения максимума протекает приблизительно по экспоненте с постоянной времени, определяемой частотой, при которой происходит изменение наклона ЛАЧХ с отрицательного на нулевой при движении по ЛАЧХ со стороны высоких частот в область средних частот.

5. Переходной процесс после достижения максимума изменяется также по экспоненте с постоянной времени, определяемой частотой, при которой происходит изменение наклона ЛАЧХ с нулевого на положительный (или с отрицательного на нулевой) при переходе из области средних частот в область низких частот. По значению этой частоты можно приближенно оценить время регулирования.

На рисунке 7.6 представлена ориентировочная картина переходного процесса, построенная из анализа ЛАЧХ на рисунке 7.5, из которого можно сделать следующие выводы:

а) установившееся значение при единичном ступенчатом воздействии равно, соответствующему ЛАЧХ при w ® 0 (L(w ®0));

б) процесс регулирования протекает с перерегулированием, величина перерегулирования пропорциональна L_max;

в) до достижения максимума переходной процесс протекает по экспоненте с постоянной времени:

(7.8)

;

г) после достижения максимума переходной процесс также изменяется по экспоненте с постоянной времени:

(7.9)

;

д) время переходного процесса ориентировочно равно:

(7.10)

t_р=(3 ¸ 5)×Т₂ +Т₃.

Дата добавления: 2014-10-23