Оптимальное управление. Постановка задачи оптимального управления. Критерии оптимальности

Синтез

Задача синтеза САУ по усл обеспечение требуемой точности в стационарном случ режиме сводится к опред-ю передаточной ф-ии системы при к-ой выполн-ся неравенство:

Если при синтезе системы по усл обеспечение требуемой точности в детерминированном стационарном режиме задача сводится к опред-ию порядка астатизма и коэфф-та передач, то при наличии случ воздействий точность системы опред-ся всей передаточной функцией системы.

Общий порядок синтеза ЧХ сводится к след-му:

1. Прежде всего находится ЧХ известной части системы (объект управления, датчики, исполнительный механизм)

2. Затем по заданным значениям спектральной плоскости входного воздействия и величине Dyдоп выходного сигнала определяется как надо скорректировать ЧХ известной части системы, чтобы обеспечить требуемую точность. На основе этого определяется ЧХ неизвестной части системы и затем определяется передаточная функция

3. Если все приложенные к системе случ воздействия явл-ся либо помехами, либо задающими воздействиями, то теоретически соответствующим выбором передаточной функции можно обеспечить любую точность системы.

Если к системе одновременно приложены оба вида воздействия(возмущение и задание), то в этом случае существует оптимальное выражение для передаточной функции, к-ая обеспечивает допустимое значение D на выходе. Эта передаточная функция однозначно определяется спектральными плотностями внешних воздействий. Эта оптимальная функция обеспечивает минимум D, меньше к-го нельзя получить не выходя за рамки линейной системы.

W_оpt(jw) - D_ymin

В этом случае не всякие требования по точности могут быть практически реализованы в лин САУ, поэтому если требования по точности достаточно жёсткие, то задача синтеза должна решаться как задача определения оптимальной передаточной функции.

Задача нахождения оптимальной передаточной фун-ии обеспечивающей максимум дисперсии выходной величины при воздействии задающего и возмущающего воздействия была решена Колмогоровым и Винером. Оптимальная передаточная фун-ия искалась при условии преобразования сигнала y=Ф₀(s)*x, где Ф₀(s) заданная желаемая передат фун-ия, при этом решалась задача обеспечения минимума отклонения y-y₀.

Полученное выражение для оптим-ой передат фун-ии в большинстве практических задач дает физически не реализуемые выражения. Из получ-го выражения выделяют физически реализуемое слагаемое и далее рассматривают только его. Нахождение опт передат ф-ии не явл-ся ещё полным решением задачи синтеза. Найденное выражение передат ф-ии следует рассматривать как предел к которому необходимо стремиться. Для завершения задачи синтеза после нахождения опт передат ф-ии надо опред-ть как выполняются и др требования предъявляемые к системе.

Под оптимальной САУ понимается наилучшая в некотором смысле система. Критерии оптимальности могут быть различны и зависят от решаемой задачи. Наиболее часто встречаются такие критерии оптимальности:

1) Точность САУ при изменяющемся воздействии,

2) Время переходного процесса,

3) Экономичность;

4) Производительность;

5) Интегральные критерии.

К настоящему времени наибольшее развитие получили 2 направления в теории оптимальности систем:

1) Теория оптимального управления движением систем с полной информацией об объекте и возмущениях;

2) Теории оптимального управления при случайных возмущениях.

Для реализации оптимального управления необходимо:

1) Определить цель управления. Цель выражается либо целевой функцией, либо критерием оптимизации.

Целевая функция или критерий оптимизации позволяют найти количественный эффект любого решения.

2) Выбрать модель для анализа и определения эффективности принятого решения.

3) Изучить все состояния среды функционирования объекта, влияющие на прошлое, настоящее и будущее процесса управления.

При решении задачи оптимального управления используются методы вариационного исчисления, принципы максимума, а также динамическое и математическое программирование.

Задачу оптимального управления в общем случае можно сформировать следующим образом:

Даны:

1)Цель управления, представленная математически в виде некоторого функционалаили критерия управления

2)Уравнения системы - они обычно задаются в виде уравнений состояний

3)Система граничных уравнений в начальный и конечный момент времени.

4)Система ограни­чений, которым должны удовлетворять переменные состояния и уравнения.

Требуется найти:

Вектор управления, при котором критерий цели управления имеет экстремум (max или min).

Необходимо отметить, что оптимальное управление в ряде случаев может не существовать, и об этом нельзя судить не решая задачу. Решение задачи нахождения оптимального управления является неоднозначным, т.е. каждое найденное решение дает локальный оптимум. Если найдены все локальные оптимумы, то в этом случае может быть выделен глобальный оптимум. Найденный глобальный оптимум является решением задачи оптимального управления.

Интегральные критерии качества:

1. Оптимальное Быстродействие

Функционал имеет вид

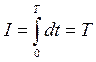
2. Оптимальная Производительность

Критерием оптимальности явл-ся угол поворота a за определенное время t и функционал имеет вид

3. Оптимальная экономичность

Критерием оптимальности явл-ся расход энергии за определенное время и функционал имеет вид

Дата добавления: 2014-10-23