Импульс тела и закон сохранения импульса

Импульсом тела (материальной точки) называется ве­личина, равная произведению массы тела на его скорость.

Обозначив импульс (его также называют иногда количеством движения) буквой 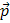, получим

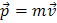. (2)

Из формулы (2) видно, что импульс — векторная ве­личина. Так как t > 0, то импульс имеет такое же на­правление, как и скорость (рис. 1).

Обозначим через 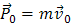импульс тела в начальный момент времени, а через 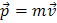— его импульс в конечный момент времени. Тогда 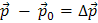есть изменение импульса тела за время ∆ t. Теперь уравнение (1) можно записать так:

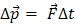(3)

Так как ∆ t > 0, то направления векторов 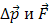совпадают. Соглас­но формуле (3) изменение импульса тела (материальной точки) про­порционально приложенной к нему силе и имеет такое же направление, как и сила.

Именно так был впервые сформу­лирован второй закон Ньютона.

Произведение силы на время ее действия называют импульсом силы. Поэтому можно сказать, что изменение импульса тела равно импуль­су действующей на него силы. Уравнение (3) пока­зывает, что одинаковые изменения импульса могут быть получены в результате действия большой силы в течение малого интервала времени или малой силы за большой промежуток времени.

Единица импульса не имеет особого названия, а ее наименование получается из определения этой величины (см. формулу (2)):

1 ед. импульса = 1 кг · 1 м/с = 1 кг · м/с.

Для нахождения импульса тела, которое нельзя счи­тать материальной точкой, поступают так: мысленно раз­бивают тело на отдельные малые элементы (материальные точки), находят импульсы полученных элементов, а потом суммируют их как векторы. Импульс тела равен сумме импульсов его отдельных элементов.

Импульс тела может быть равен нулю даже в том слу­чае, когда оно движется. Примером может служить вра­щающийся вокруг неподвижной оси однородный диск. Действительно, два диаметрально противоположных, рав­ных по массе элемента А и В имеют одинаковые по моду­лю скорости (рис. 5.2). Следовательно, их импульсы рав­ны по модулю, но противоположно направлены: 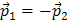, поэтому 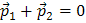. Такие равенства справедливы для любых двух диаметрально противоположных элементов диска.

Второй закон Ньютона может быть записан в импульс­ной форме: изменение импульса тела равно импульсу дей­ствующей на него силы.

Закон сохранения импульса является следствием вто­рого и третьего законов Ньютона.

Для простоты будем считать, что система состоит всего из двух тел. Это могут быть две звезды, два бильярдных шара или два других тела.

Силы, возникающие в результате взаимодействия тела, принадлежащего системе, с телом, не принадлежащим ей, называются внешними силами. Если рассматривать систему, состоящую из двух бильярдных шаров, то сила взаимодействия шаров с краем стола при ударе о него, сила трения шара о поверхность стола — внешние силы. Пусть на тела системы действуют внешние силы .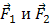

Силы, возникающие в результатевзаимодействия тел, принадлежащих системе, называются внутренними силами. Обозначим их через 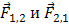(рис. 3). По третьему закону Ньютона 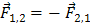.Отсюда следует, что сумма внутренних сил всегда равна нулю:

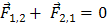. (4)

Вследствие действия сил на тела системы их импульсы изменяются. Если взаимодействие рассматривается за ма­лый промежуток времени Δ t, то для тел системы можно записать второй закон Ньютона в виде

_-

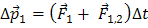
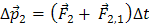Сложив эти равенства, получим

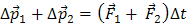. (5)

В левой части равенства (5) стоит сумма изменений импульсов всех тел системы, т. е. изменение импульса са­мой системы (под импульсом системы мы будем понимать геометрическую сумму импульсов всех тел системы):

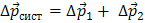. (6)

Учитывая равенство (5), можно равенство (6) запи­сать так:

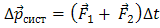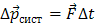, . (7)

где 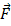— геометрическая сумма всех внешних сил, действу­ющих на тела системы.

Мы доказали весьма важное положение: импульс сис­темы тел могут изменить только внешние силы, причем изменение импульса системы 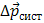совпадает по направ­лению с суммарной внешней силой. Внутренние силы из­меняют импульсы отдельных тел системы, но изменить суммарный импульс системы они не могут.

Уравнение (7) справедливо для любого интервала вре­мени Δ t, если сумма внешних сил остается постоянной.

Из уравнения (7) вытекает закон сохранения импуль­са. Если внешние силы на систему не действуют или их сумма равна нулю, то 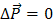и импульс системы остается неизменным, или, как говорят, сохраняется:

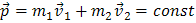. (8)

Закон сохранения импульса формулируется так: если сумма внешних сил равна нулю, то импульс системы тел сохраняется. Иначе говоря, в этом слу­чае тела могут только обмениваться импульсами, суммар­ное же значение импульса не изменяется.

Импульс, очевидно, сохраняется в изолированной сис­теме тел, так как в этой системе на тела вообще не дейст­вуют внешние силы. Но область применения закона сохра­нения импульса шире: если даже на тела системы действуют внешние силы, но их сумма равна нулю (т. е. система является замкнутой), то импульс системы все равно сохраняется.

Полученный результат справедлив для системы, содер­жащей произвольное число тел:

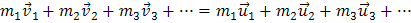, (9)

где 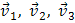, … — скорости тел в начальный момент времени; 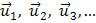— скорости тел в конечный момент.

Так как импульс — векторная величина, то уравне­ние (9) представляет собой компактную запись трех уравнений для проекций импульсов системы на оси коор­динат.

Если сумма внешних сил не равна нулю, но сумма про­екций сил на какое-то направление равна нулю, то проек­ция суммарного импульса системы на это направление не меняется. Например, систему тел на Земле или вблизи по­верхности Земли нельзя считать изолированной, так как на тела действует внешняя сила — сила тяжести. Однако вдоль горизонтального направления сила тяжести не дей­ствует и сумма проекций импульсов тел на это направле­ние будет оставаться неизменной, если действием сил тре­ния можно пренебречь.

В изолированной системе тел импульс системы сохра­няется. Также он может сохраняться в случае, если сумма внешних сил, действующих на систему, равна нулю.

Дата добавления: 2014-10-23