Гармонические колебания (уравнение, характеристика, график)

Колебания, возникающие под действием внешних, периодически изменяющихся сил (при периодическом поступлении энергии извне к колебательной системе)

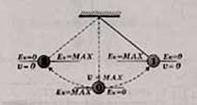
Превращение энергии

Пружинный маятник

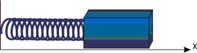
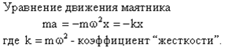
Циклическая частота и период колебаний равны, соответственно:

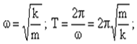
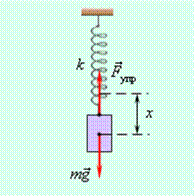Материальная точка, закрепленная на абсолютно упругой пружине

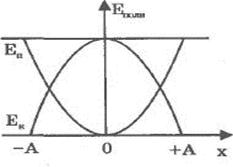
Ø график зависимости потенциальной и кинетической энергии пружинного маятника от координаты х.

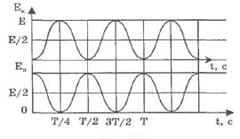
Ø качественные графики зависимостей кинетической и потенциальной энергии от времени.

Ø Вынужденные

Ø Частота вынужденных колебаний равна частоте изменения внешней силы

Ø Если Fbc изменяется по закону синуса или косинуса, то вынужденные колебания будут гармоническими

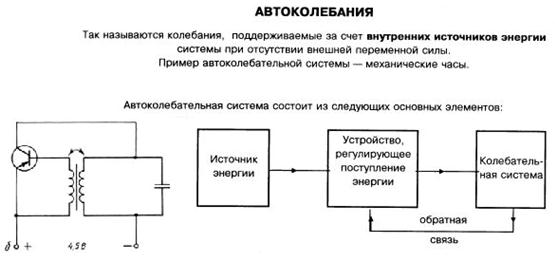
Ø При автоколебаниях необходимо периодическое поступлении энергии от собственного источника внутри колебательной системы

Гармонические колебания – это колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса

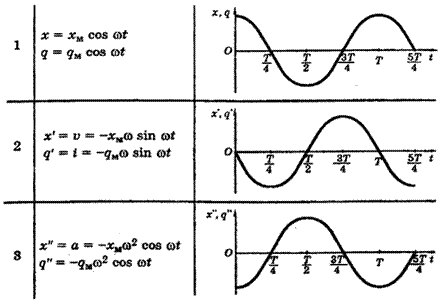
• уравнения гармонических колебаний (законы движения точек) имеют вид

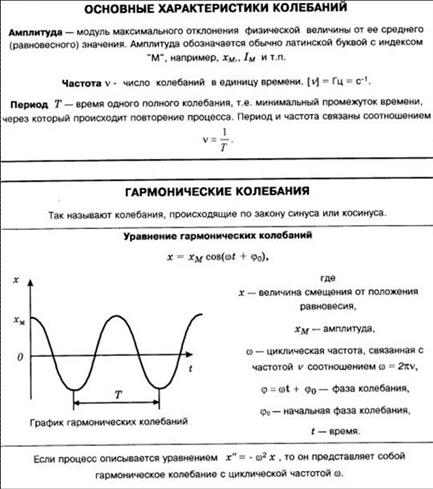
Гармоническими колебаниями называются такие колебания, при которых колеблющаяся величина меняется от времени по закону синуса или косинуса.
Уравнение гармонических колебаний имеет вид:

,
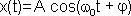где A - амплитуда колебаний (величина наибольшего отклонения системы от положения равновесия); 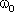- круговая (циклическая) частота. Периодически изменяющийся аргумент косинуса 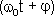- называется фазой колебаний. Фаза колебаний определяет смещение колеблющейся величины от положения равновесия в данный момент времени t. Постояннаяφ представляет собой значение фазы в момент времени t = 0 и называется начальной фазой колебания. Значение начальной фазы определяется выбором начала отсчета. Величина x может принимать значения, лежащие в пределах от -A до +A.
Промежуток времени T, через который повторяются определенные состояния колебательной системы, называется периодом колебаний. Косинус - периодическая функция с периодом 2π, поэтому за промежуток времени T, через который фаза колебаний получит приращение равное 2π, состояние системы, совершающей гармонические колебания, будет повторяться. Этот промежуток времени T называется периодом гармонических колебаний.
Период гармонических колебаний равен: T = 2π/.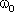
Число колебаний в единицу времени называется частотой колебаний ν.
Частота гармонических колебаний равна: ν = 1/T. Единица измерения частоты герц (Гц) - одно колебание в секунду.
Круговая частота 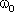= 2π/T = 2πν дает число колебаний за 2π секунд.

Обобщенное гармоническое колебание в дифференциальном виде

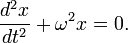
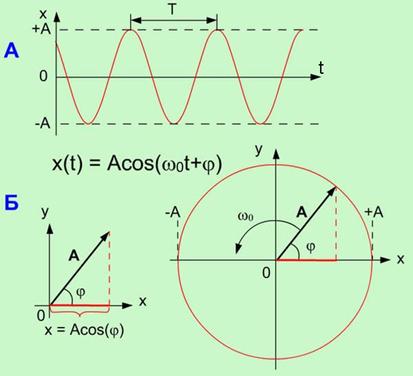
Графически гармонические колебания можно изображать в виде зависимости x от t (рис.1.1.А), так и методом вращающейся амплитуды (метод векторных диаграмм) (рис.1.1.Б).

Рисунок 1.1. Графическое изображение гармонических колебаний

Метод вращающейся амплитуды позволяет наглядно представить все параметры, входящие в уравнение гармонических колебаний. Действительно, если вектор амплитуды А расположен под углом φ к оси х (см. Рисунок 1.1. Б), то его проекция на ось х будет равна: x = Acos(φ). Угол φ и есть начальная фаза. Если вектор А привести во вращение с угловой скоростью 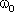, равной круговой частоте колебаний, то проекция конца вектора будет перемещаться по оси х и принимать значения, лежащие в пределах от -A до +A, причем координата этой проекции будет меняться со временем по закону:
.
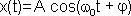Таким образом, длина вектора равна амплитуде гармонического колебания, направление вектора в начальный момент образует с осью x угол равный начальной фазе колебаний φ, а изменение угла направления от времени равно фазе гармонических колебаний. Время, за которое вектор амплитуды делает один полный оборот, равно периоду Т гармонических колебаний. Число оборотов вектора в секунду равно частоте колебаний ν.

Дата добавления: 2014-10-23