Перенос заряженных частиц через мембрану

Пассивный транспорт ионов.

1.
В том случае, когда изменяется концентрация вещества и электрический потенциал, уравнения для потоков незаряженных и заряженных частиц сходны: Φ = – uc (dG/dx).

2.
Если изменяется еще и стандартный электрохимический потенциал, то уравнение для потока вещества описывается уравнением Теорелла: Φ = – cu • (dμ/dx), где μ – электрохимический потенциал, который зависит от природы вещества и природы растворителя.

3.
Если во всей рассматриваемой области диффузии отсутствуют химические превращения вещества и растворитель одинаков, то в этом случае уравнение Теорелла сводится к электродиффузному уравнению Нернста-Планка: Φ = –uRT (dc/dx) –cuz• Fdφ/dx. Это уравнениеописывает пассивный перенос частиц в условиях существования градиентов концентрации вещества и электрического потенциала в растворе или в однородной незаряженной мембране.

4.
Если известны концентрации ионов по обе стороны мембраны, трансмембранная разность потенциалов и коэффициент проницаемости, то величину пассивного потока ионов описывают с помощью уравнения Гольдмана: Φ ={zFΔφΡ/RT} • {[c₂exp(zFΔφ/RT) -c₁]/[1-exp(zFΔφ/RT]}.

5.
Если потоки направлены противоположно, то их отношение описывается уравнением Уссинга-Теорелла: Φ₂/Φ₁ = c₁/c₂exp[- zFΔφ/RT].

Вывод: пассивный транспорт ионов может происходить только в случае наличия на мембране градиентов концентрации или электрического потенциала и описывается в общем случае уравнениями Нернста-Планка, Гольдмана или Уссинга-Теорелла. Невыполнение этих уравнений свидетельствует о том, что перенос ионов осуществляется активно или через мембранные каналы, где невозможно существование независимых ионных потоков.

Уравнение Нернста. В живом организме по обе стороны любой биологической мембраны находятся ионные растворы, причем концентрации одного и того же иона по обе стороны часто отличаются. Одной из причин установления и поддержания этих градиентов концентраций является различная проницаемость мембраны для тех или иных ионов. В этом случае градиент концентрации одного вещества может поддерживаться за счет наличия градиента концентрации другого вещества и/или разности потенциалов по обе стороны мембраны (так называемой трансмембранной разности потенциалов). Условием установления равновесия между двумя растворами, разделенными полупроницаемой мембраной, с различными концентрациями одинаковых ионов является равенство электрохимических потенциалов по одну и другую сторону мембраны. Значение разности электрических потенциалов, которая устанавливается на мембране при наличии градиента концентраций, рассчитывается с помощью уравнения Нернста: Δφ = φ_i - φ₀ = (RT/zF)•lg (c₀/c_i).

Уравнение Фика описывает как пассивный транспорт незаряженных частиц, так и пассивный транспорт заряженных частиц в отсутствии электрического поля. Рассмотрим теперь транспорт ионов с учетом электрического поля внутри мембраны.

На отдельный ион в электрическом поле действует сила f₀ = qE, где Е - напряженность электрического поля, а q = Ze - заряд иона (Z - валентность иона). Напряженность поля выражается через градиент

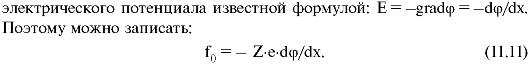Уравнению 11.11 можно придать более удобный вид, умножив обе его части на постоянную Авогадро (N_A):Это уравнение Нернста-Планка (электродиффузное уравнение). Оно устанавливает зависимость плотности диффузного потока ионов от концентрации ионов и от градиента потенциала (dφ/dx).

Для нейтральных частиц (Z = 0) уравнение Нернста-Планка переходит в уравнение Фика.

Равновесие Доннана. В клетке кроме малых ионов находятся еще и заряженные макромолекулы (белки, нуклеиновые кислоты). Как правило, эти макромолекулы заряжены отрицательно. Мембрана проницаема для малых ионов и непроницаема для макромолекул. Для каждого из растворов, находящихся по обе стороны мембраны, необходимо выполнение условия электронейтральности, то есть сумма положительных и отрицательных зарядов всех ионов должна равняться нулю. Для компенсации внутри клетки отрицательных зарядов макромолекул часть отрицательных малых ионов выходит из клетки, а часть положительных зарядов проходит в клетку из межклеточной среды. То есть на мембране возникает так называемая доннановская разность потенциалов, которая составляет φ_i - φ₀ = -RT/F•[R^-]_i /2c.

Ионный транспорт через каналы. Механизм обычной электродиффузии в живой клетке обеспечивает проницаемость мембран для кислорода и углекислого газа. Этот процесс происходит слишком медленно и плохо контролируется, поэтому клетка не может его использовать для переноса питательных веществ и необходимых для жизнедеятельности ионов. Так, из каждых 10⁶¹ ионов, находящихся в водном растворе, только один находится в липидной фазе мембраны. Скорость переноса ионов значительно возрастает, если в мембране существуют ионные каналы. Наиболее распространены каналы для ионов калия, натрия, кальция. Ионные мембранные каналы образованы интегральными белками. Такой канал может быть либо открыт, либо закрыт для транспорта ионов. Эти два состояния реализуются изменением конформации каналообразующих белков, что может быть вызвано изменением условий в клетке и во внеклеточной среде, например, изменением мембранного потенциала.

Так как обычно с помощью каналов транспортируются гидрофильные вещества, то во внутренней полости их имеется большое число гидрофильных химических групп. Каждый канал неоднороден по строению: вдоль его внутренней полости располагаются различные химические группы, сродство ионов к которым неодинаково. Канал может иметь один или несколько ионных центров связывания. Эти центры представляют собой заряженные группы. Когда ион попадает в канал, он связывается с этими группами и таким образом попадает в потенциальную яму. Для того чтобы попасть в другую потенциальную яму, иону требуется преодолеть некоторый потенциальный барьер. Таких барьеров вдоль длины канала может быть несколько, причем высота их, обычно, неодинакова и может изменяться в зависимости от наличия или отсутствия ионов в канале, или изменения трансмембранной разности потенциалов. Так как в канале находятся заряженные группы, то изменение мембранного потенциала является нелинейным. Кроме этого, наличие заряженных групп может привести к непостоянству значений коэффициента распределения по длине канала.

Многие мембранные каналы настолько узки, что ионы не могут в них двигаться в различных направлениях независимо друг от друга: если в какой-либо потенциальной яме уже есть ион, то другой не может в неё попасть. Это относится, например, к калиевым каналам. Встречные потоки ионов натрия через натриевые каналы можно считать независимыми, но если через эти каналы движутся ионы калия, то принцип независимости уже не выполняется. Для многих каналов, в зависимости от их строения, при высоких концентрациях ионов в окружающей среде наблюдается а) э ф ф е к т н а с ы щ е н и я: при увеличении концентрации ионов скорость их переноса повышается, но только до определенного уровня, выше которого скорость не изменяется; б) б л о к и р о в к а: при концентрациях ионов выше некоторого значения скорость переноса начинает снижаться.

При переходе иона из окружающей среды в канал свободная энергия уменьшается. При этом величина потенциального барьера ниже, чем при переходе иона непосредственно через липидный бислой мембраны.

Ионные каналы обладают селективностью, то есть имеют различные величины проводимости для различных ионов. Каждый канал транспортирует преимущественно ионы одного вида, например, натриевый канал – ионы натрия, калиевый – ионы калия. Через катионные каналы не способны проходить анионы и наоборот. Но для ионов того же знака, что и основной ион, канал уже не обладает такой абсолютной селективностью. Проводимость канала для других ионов своего знака ниже, чем для собственного, но отлична от нуля. Например, через специфические натриевые каналы способны транспортироваться также и ионы калия, но в 20 раз медленнее, чем ионы натрия.

Согласно современным представлениям, селективность канала, прежде всего, определяется радиусом транспортируемого иона. Ионы, радиус которых превышает радиус канала, не способны проходить через канал вследствие такого стерического несоответствия. Ионы, обладающие меньшим радиусом, по сравнению с радиусом канала, также не всегда могут пройти через канал. Чем меньше радиус иона по сравнению с радиусом канала, тем меньше вероятность прохождения иона через этот канал. Этот эффект объясняется тем, что ионы в водном растворе всегда находятся в гидратированном состоянии. Перенос же через канал требует сброса нескольких гидратных оболочек, в результате которого ион остается лишь в одной гидратной «одежке». Сброшенная гидратная оболочка заменяется другими полярными соединениями, в роли которых выступают фиксированные дипольные группы канала. Размер иона должен быть таковым, чтобы он мог взаимодействовать с оптимальным числом этих полярных групп. Например, ион калия в своем селективном канале взаимодействует со всеми пятью атомами кислорода, а меньший по размеру ион натрия может связаться в калиевом канале только с двумя атомами кислорода. Следовательно, прочность связи канала с ионом натрия будет минимальна. А если связи иона с дипольными группами нет совсем, то и пройти он через этот канал не может. Следовательно, лучше всего проходит через канал тот ион, который имеет радиус (вместе с одинарной гидратной «одежкой») равный радиусу канала.

Селективность каналов определяется не только зависимостью проводимости канала от радиуса транспортируемого иона, но и химическим строением иона. Например, через натриевые каналы переносятся ионы гидроксиламмония и не переносятся ионы метиламмония, хотя их радиусы равны радиусу канала. Это объясняется тем, что гидроксильная группа гидроксиламмония способна образовывать водородные связи с атомами кислорода, выстилающими внутренний диаметр канала, а метильная группа метиламмония с ними не взаимодействует.

Каналы могут блокироваться некоторыми соединениями, которые связываются с селективными фильтрами или с входом в канал, закупоривая его. Так как молекула-блокатор должна стерически соответствовать участку блокируемого канала, то для каналов определённого вида существуют специфические блокаторы. Например, молекулы тетродоксина блокируют натриевые каналы, а молекулы тетраэтиламмония – калиевые.

Дата добавления: 2014-10-23