Хлеб для Васи

Рис. 15.4.

«Ящик Эджворта»

ной эффективности является Парето-оптимальность, и возможность ее достижения - серьезное преимущество рыночной системы по сравне­нию с командно-административной.

Очень важно, что эффективность распределения по Парето предпо­лагает максимизацию общественной полезности, хотя и является соци­ально нейтральным критерием. Поэтому равноправное (об этом поня­тии подробнее будет сказано далее), но отнюдь не равное распределе­ние при достижении наибольшей суммарной полезности в рыночной системе корректируется через перераспределительную систему, т. е. с помощью государства.

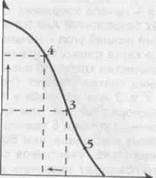
Но как максимизируется общественное благосостояние? Это один из главных вопросов неоклассической теор ии эконо ми к и б лаго с о ст оя­н и я, предметом которой является создание модели экономического оп­тимума и решение проблемы соотношения между эффективностью эко­номической системы и справедливостью распределения. Отправным пунктом в исследовании возможности максимизировать благосостояние является модель, называемая «ящ и к Эджвор т а» (рис. 15.4). Данная модель представляет собой диаграмму полезностей двух контрагентов и помогает выявить условия достижения оптимального распределения экономических благ, при обмене которыми достигается максимальная полезность участников обмена.

Рассмотрим модель обмена двумя товарами между двумя потреби­телями, например, Аней и Васей, которые олицетворяют две обществен­ные группы. На рис. 15.4 изображены две системы координат, поверну­тые друг к другу так, что их оси составляют прямоугольник. Правый вер-

и недостатки рыночного механизма

хний угол прямоугольника - начало координат 0_А, в системе которых расположена карта кривых безразличия Ани (сравните с аналогичными картами в гл. 5, § 9). Левый нижний угол - начало координат О_в, в сис­теме которых расположена карта кривых безразличия Васи. По горизон­тальной оси отмечено количество хлеба, по вертикальной - шоколада, в количестве 10 и 6 единиц соответственно. Пусть изначально блага распределены в точке 1, т. е. 7 единиц хлеба и 1 единица шоколада у Васи (поэтому он ценит шоколад больше, чем хлеб). В той же точке 1 мы видим, что у Ани 3 единицы хлеба и 5 единиц шоколада¹ (она, имея больше шоколада, оценивает хлеб выше, чем Вася). В этой точке пре­дельные нормы замещения (MRS) участников сделки не совпадают²: MRS = 3, MRS_B = 1/2, что позволяет заключать взаимовыгодные сдел­ки. Кривые безразличия U_M и U_BV соответствующие набору предпочте­ний Ани и Васи, пересекаются в точке 1, образуя область взаимовыгод­ных сделок (заштрихованная часть рисунка). Однако не при каждой вза­имовыгодной сделке распределение эффективно. Например, в точке 2 сделка взаимовыгодна (Вася приобретет дополнительную плитку шоко­лада, а Аня - еще одну буханку хлеба, т. е. то, что они больше ценят). Но так как кривые безразличия в этой точке пересекаются, предельные нормы замещения (MRS) у контрагентов не равны. Условием же эффек­тивного распределения является равенство MRS участников обмена, в результате которого благосостояние контрагентов нельзя улучшить, не ухудшив положения одного из них, т. е. условие Парето-эффективного распределения. Оно изображено на рис. 15.4 в точках 3, 4 и 5, в кото­рых кривые безразличия касаются друг друга и имеют в этих точках оди­наковый наклон. Следовательно, MRS_A = MRS_B. Данное правило распро­страняется и на множество контрагентов, обменивающихся множеством товаров: распределение эффективно только в том случае, если MRS любой пары товаров одинаковы для всех участников обмена. Таким об­разом, одновременное равновесие участников обмена устанавливается при заключении эффективной сделки:

1)Примем за единицу измерения хлеба 1 буханку, а для шоколада -1 плитку. 2В этом легко убедиться: про­ ведите через точку 1 касательные к соответствующей кривым безразличия Ани и Васи. Вы увидите, что у них разный наклон Касательная к кривой безразличия Чл имеет наклон -3, а наклон касательной к кривой безрачия ив равен -1/2

MRS_A шок., хл.= (Р шок. / Р хл.) = MRS_B шок., хл. (3)

Данная формула отражает условие

достижения равновесия на конкурентных

рынках. Конкурен т ны м равнове с ие м

экономисты называют равновесие по

Вальрасу. Напомним, что в основе

достишения конкурентного равновесия

лежит установление такого набора цен, при

котором спрос равен предложению на

всех имеющихся рынках в условиях кон-

куренции. вернемся к рис. 15.4. Кривая, прохо.

Глава 15

и недостатки рыночного механизма

Полезность, Дни и₂

и,

Рис. 15.6.

U U 2 Uj Полезность

Васи

Рис. 15.5. Кривая достижимой (возможной) полезности

дящая из точки 0_А в точку 0_В соединяет все точки касания кривых без­различия контрагентов Ани и Васи, в которых их предельные нормы за­мещения равны. Такая кривая, отражающая все эффективные сделки, т. е. все случаи эффективного распределения, называется кр и вой кон­трак т ов. Именно кривая контрактов и служит графическим изображени­ем Парето-эффективного распределения между двумя агентами или двумя группами агентов, что и отражено на рис. 15.4.

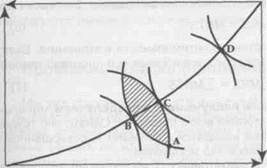
На рисунке 15.5 изображена кривая контрактов, вогнутая по отноше­нию к началу системы координат. Она представляет собой известную нам кривую из «ящика Эджворта» (рис. 15.4), полученную при проведе­нии линии через все точки касания кривых безразличия (точки 4, 3, 5). Любая точка этой кривой представляет собой эффективное распреде­ление по Парето, максимизирующее суммарную полезность распреде­ления благ в обществе. Иначе говоря, это кривая достижимой полезнос­ти для общества. Допустим, что все общество состоит из двух лиц, Ани и Васи, олицетворяющих две общественные группы. При продви­жении из точки 3 в точку 4 полезность благ для одной группы обще­ства, которую представляет Вася, уменьшается. Напротив, полез­ность для другой группы, которую олицетворяет Аня, возрастает. Но в какой точке на кривой достижимой полезности максимизируется об­щественное благосостояние? Ведь эффективное по Парето распре­деление не дает ответа на вопрос о распределении благосостояния между людьми с точки зрения его желательности для общества. Даже самые крайние точки на кривой достижимой полезности, когда всё дос­тается какому-либо одному из субъектов (или одной общественной груп­пе), Парето-оптимальны.

Максимизация общественного благосостояния

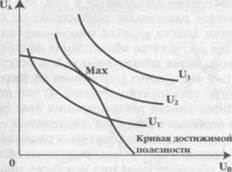
Обратимся к рис. 15.6.

Кривая достижимой полезности (рис. 15.6) показывает все варианты полезности, достижимой при Парето-эффективном распределении дан­ного количества благ между двумя членами общества (как в примере с «ящиком Эджворта») или общественными группами.

Выпуклыми по отношению к началу системы координат изображены новые для нас графики - общественные кривые безразличия, или кри­вые равного благосостояния. О бщ е ст венная кр и вая б езразлич и я, по аналогии с индивидуальной кривой безразличия (см. гл. 5, § 9), показы­вает все комбинации полезностей различных социальных групп, соот­ветствующих одному и тому же уровню общественного благосостояния, а поэтому одинаково приемлемых (одинаково безразличных) для обще­ства. Существует множество общественных кривых безразличия (карта общественных кривых безразличия), которые обозначают разные уров­ни благосостояния общества. Чем выше уровень благосостояния, тем дальше соответствующая ему общественная кривая безразличия распо­ложена от начала координат. Однако самый высокий уровень благосос­тояния, которого общество может реально достичь при заданных воз­можностях, отражает та общественная кривая безразличия, которая имеет только одну общую точку (или общую касательную) с кривой дос­тижимой полезности. Таким образом, распределение, максимизирующее общественное благосостояние, будет достигнуто в точке касания общественной кривой безразличия и кривой достижимой полезности.

Рассмотренный нами пример еще раз показывает универсальный характер аппарата известных нам кривых безразличия, используемый ^пРи анализе проблем выбора.

В связи с проблемой максимизации общественного благосостояния Рассмотрим две теоремы экономики благосостояния. Первая т еоре м а

механизма

Преимущества и недостатки рыночного

Труд для производства шоколада

Капитал для производства шоколада

Капитал для производства хлеба

Рис. 15.7.

Глава 15

эконо ми к и благо с о с тоян и я заключается в том, что распределение в условиях конкурентного равновесия эффективно по Парето. Значит если всем участникам сделки удается максимизировать свою полез­ность, то в результате достигается общественно эффективное распре­деление, максимизирующее общественное благосостояние. Данная теорема указывает на инструмент достижения эффективности по Па­рето: это - механизм конкурентного рынка. С его помощью можно достичь Парето-эффективного распределения благ среди сотни ты­сяч участников, не прибегая к созданию специальных структур по сбо­ру информации и принятию централизованных решений. Необходимо и достаточно, чтобы каждый участник распределения обладал информа­цией о конкурентной рыночной цене того или иного товара.

В т орая теорема эконо ми ки б лагосо ст оян и я гласит, что в опреде­ленных условиях¹ при Парето-эффективном размещении благ может быть достигнуто конкурентное равновесие. Иными словами, каждая точ­ка кривой контрактов - это случай конкурентного равновесия. Данная теорема проводит разграничение между аллокативной и дистрибутив­ной ролью ценового сигнала (подробнее об этих функциях см. гл. 5, § 10). С одной стороны, рыночная цена определяет относительную редкость того или иного блага, с другой, - показывает, какой объем различных товаров каждый рыночный агент в состоянии приобрести.

¹ Условие, при котором вы­полняется вторая теорема бла­госостояния, заключается в том, что предпочтения участников распределения должны выра­жаться кривыми безразличия, имеющими такую же форму, как в модели «ящик Эджворта», т. е. выпуклыми. Тогда между парой кривых безразличия пройдет единственная общая касатель­ная, которую можно представить в виде общего бюджетного огра­ничения для двух участников распределения, что говорит о до­стижении равновесия каждого из них. Если же кривые безразличия участников распределения будут иметь другую форму (например, волнистую), не позволяющую провести между ними общую ка­сательную, то равновесия при Парето-эффективном распреде­лении достигнуто не будет.

Однако для достижения общей эф­фективности экономики недостаточно эффективного распределения благ среди потребителей. Необходимо, чтобы и про­изводители распоряжались экономичес­кими благами эффективно.

Для рассмотрения условий эффек­тивного использования факторов произ­водства можно вновь использовать «ящик Эджворта». Рассмотрим рис. 15.7. На повернутых друг к другу осях координат расположены факторы произ­водства хлеба и шоколада. Каждая точка диаграммы показывает затраты труда и капитала для производства этих двух товаров.

Набор изоквант показывает уровни выпусков хлеба и шоколада при различ­ных комбинациях затрат труда и капита­ла (рис. 15.7.). Распределение факторов производства эффективно, если выпуск

Дата добавления: 2014-10-23