Связь напряженности и потенциала

Потенциал. Работа перемещения заряда в ЭСП.

Потенциал – энергетическая характеристика ЭСП, в данной точке поля равная отношению

(14)

где 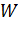– потенциальная энергия пробного заряда , помещенного в данную точку ЭСП.

В поле точечного заряда потенциал точки, находящейся на расстоянии от заряда:

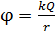, (15)

где 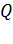– заряд, создающий поле.

Потенциал – алгебраическая величина, его знак равен знаку заряда 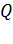, создающего поле (см. формулу (15)). Потенциал ЭСП, созданного в данной точке несколькими зарядами (точечными, а также и распределенными по длине или по поверхности заряженных тел) равен алгебраической сумме потенциалов 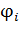полей всех заряженных тел в этой точке:

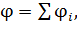(16)

Работа по перемещению точечного заряда 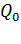из точки 1 в точку 2 в электростатическом поле определятся формулой:

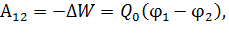(17)

где 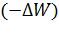– убыль потенциальной энергии заряда 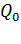; 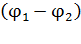– разность потенциалов начальной и конечной точек для заряда, перемещающегося в ЭСП.

Потенциал связан с напряженностью ЭСП следующим соотношением:

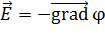, (18)

где 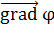– вектор градиента потенциала.

Проекция вектора напряженности 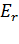на направление вектора градиента потенциала

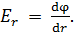(19)

Здесь 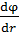– модуль градиента потенциала.

В однородном ЭСП, в котором вектор напряженности одинаков во всех точках поля, модуль напряженности

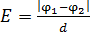, (20)

где 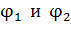– потенциалы точек двух эквипотенциальных поверхностей; 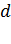– расстояние между этими поверхностями по нормали к ним, т. е. вдоль силовой линии ЭСП.

Таким образом, имеется три способа расчета напряженности электростатического поля:

1) С помощью принципа суперпозиции, применяемого в следующих случаях:

а) для системы точечных зарядов – по формуле (6), (см. рис. 3);

б) поле создано несколькими заряженными телами, например: нить и точечный заряд; две плоскости; плоскость и нить и т. п., – также по формуле (6);

в) для распределенного заряда – по формуле (7).

Этим методом удается найти, как правило, только значение напряженности в одной выбранной точке; лишь в отдельных случаях, например, для ЭСП, созданного электрическим диполем, можно найти зависимость 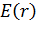, т. е. напряженность поля как функцию расстояния от зарядов.

2) С помощью теоремы Гаусса – по формуле (9), для полей, обладающих симметрией (сферической, осевой или зеркальной). Для таких полей метод позволяет найти функцию 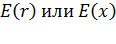– зависимость напряженности от расстояния от центра (оси) симметрии поля.

3) С использованием формулы связи 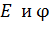– по формулам (19) и (20). Если известна зависимость 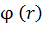, то можно, используя формулу (19), путем дифференцирования найти функцию 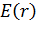. По формуле (20) находят численное значение напряженности , которое одинаково во всех точках однородного ЭСП.

Дата добавления: 2014-10-23