Способи зображення синусоїдних величин

1. Аналітичний – запис у вигляді тригонометричної функції. Використання аналітичного методу дозволяє виконувати розрахунки зі встановленою точністю. Цей метод був запропонований американським вченим Штейнмецом і базується на використанні комплексних чисел для зображення синусоїдних функцій.

2. Графічний – графіки також називаються часовими діаграмами(див. рис. 5.1);

3. Векторний – у вигляді векторної діаграми.

Векторне зображення синусоїдних величин

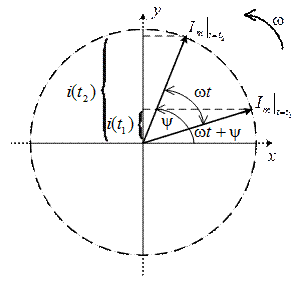
На декартовій площині з початку координат проводять вектори, рівні по модулю амплітудним значенням синусоїдних величин, і обертають ці вектори проти годинникової стрілки (такий напрямок прийнято за позитивний) з кутовою частотою, рівної ω. Фазовий кут при обертанні відраховується від позитивної півосі абсцис. Проекції обертових векторів на вісь ординат дорівнюють миттєвим значенням ЕРС е ₁й е ₂ (рис. 5.2, б).

Сукупність векторів, що зображують синусоїдно-змінні ЕРС, напруги й струми, називають векторною діаграмою.

При побудові векторних діаграм вектори зручно розташовувати для початкового моменту часу (t= 0),що випливає з рівності кутових частот синусоїдних величин й еквівалентно тому, що Декартова система координат сама обертається за годинниковою стрілкою зі швидкістю ω. Таким чином, у цій системі координат вектори нерухомі (рис. 5.3, б). Векторні діаграми знайшли широке застосування при аналізі електричних кіл синусоїдного струму. Їхнє застосування робить розрахунок електричного кола більше наочним і простим. Це спрощення полягає в тому, що додавання й віднімання миттєвих значень величин можна замінити додаванням і відніманням відповідних векторів.

При аналізі кіл частіше застосовують векторні діаграми діючих значень, на яких довжина вектора дорівнює у масштабі не амплітудному, а діючому значенню напруги, струму, ЕРС. У такому випадку обертання векторів втрачає свою суть, бо за їх допомогою вже не можна знаходити миттєві значення.

а)	б)
Рис. 5.2. Побудова векторних діаграм

Нехай, наприклад, у вузлі розгалуженого кола (рис. 5.3) загальний струм i ₃ дорівнює сумі струмів i ₁й i ₂ двох гілок:

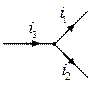
Рис. 5.3. Зображення вузла розгалуженого кола зі струмами

Кожний із цих струмів синусоїдний і може бути представлений рівнянням

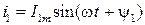та .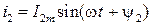

Результуючий струм також буде синусоїдний:

.

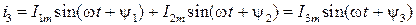Визначення амплітуди 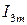і початкової фази 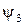цього струму шляхом відповідних тригонометричних перетворень виходить досить громіздким і мало наочним, особливо, якщо додається велика кількість синусоїдних величин. Значно простіше це здійснюється за допомогою векторної діаграми.

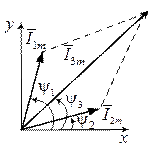
Рис. 5.4. Використання векторної діаграми
для розрахунку сумарного струму

На рис. 5.4 зображені початкові положення векторів струмів, проекції яких на вісь ординат дають миттєві значення струмів для t= 0.При обертанні цих векторів з однаковою кутовою швидкістю ωїхнє взаємне розташування не змінюється, і кут зсуву фаз між ними залишається рівним .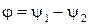

Оскільки алгебрична сума проекцій векторів на вісь ординат дорівнює миттєвому значенню загального струму, вектор загального струму дорівнює геометричній сумі векторів струмів:

_.

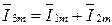Побудова векторної діаграми в масштабі дозволяє визначити значення 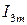й 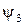з діаграми, після чого може бути записаний вираз для миттєвого значення 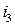шляхом формального врахування кутової частоти:

.

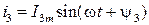Векторні діаграми поділяють на прості та топографічні, які зазвичай використовуються для напруг.

На топографічній діаграмі кожний наступний вектор відкладають із кінця попереднього у такій послідовності, як з’єднані елементи кола.

Подання синусоїдних ЕРС, напруг і струмів комплексними числами

Геометричні операції з векторами можна замінити алгебричними операціями з комплексними числами, що істотно підвищує точність одержуваних результатів.

Коли початок вектора сумістити з початком координат комплексної площини, то цей вектор можна записати комплексним числом 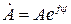, де модуль комплексного числа дорівнює довжині вектора, а аргумент вектора – куту вектора з віссю дійсних значень.

Проекцією вектора на вісь дійсних чисел називають дійсною частиною комплексного числа і позначають 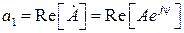, проекцію на вісь умовних чисел – умовною частиною і позначають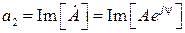

Кожному вектору на комплексній площині відповідає певне комплексне число, що може бути записане в:

показниковій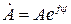

тригонометричній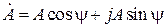

Дата добавления: 2014-10-23