ПРИМЕР. Компьютерная реализация схемы распределения ресурсов приближенных аналитическим методом

Методика построения математических моделей динамики перераспределения ресурсов может базироваться на подходе, позволяющим использовать приближенное аналитическое решение системы обыкновенных дифференциальных уравнений компактная запись системы обыкновенных дифференциальных уравнений, описывающих динамику расхода и накопления ресурсов(при заданной схема распределения) может иметь вид

(1) x_i = k_i (x(t))*x_i(t) + q_i(x(t)), i=

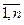
где x_i(0), i=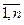- концентрат ресурсов заданы

k_i (x(t)) и q_i(x(t)) могут быть представлены следующими выражениями

k_i (x(t)) = 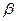_ii + 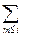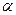_im x_m(t)

q_i(x(t)) = - формула на листе

данная система выражает материальный баланс, при этом составляющие k_i (x(t)) – есть сток I – того продукта, q_i(x(t)) – есть источник в i-том узле дерева(схемы распределения).

Пусть задана схема распределения

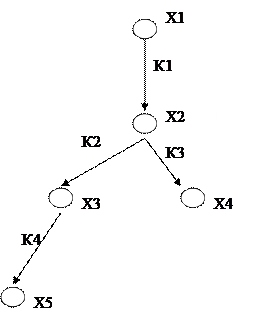Где х1, …, х5 – количество(концентрации) продуктов в следующих узлах, пунктах, к1, …, к2 – константы скорости распределения. Динамика расхода и накопления продуктов х1, …, х5 описывается системой вида

2)

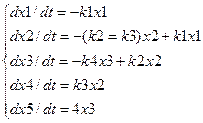
Дальнейшее преобразование системы (2) связанно с линейной аппроксимацией выражений k_i (x(t)) и q_i(x(t)) на заданном временном отрезке с помощью временных функций. Это в свою очередь позволяет записать систему (2) в виде

(3)

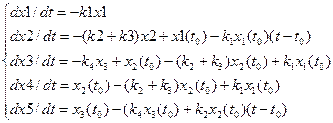
В выражении 3 величины со знаком (-) определяются ч/з функции источников q_i(x(t)), а со знаком (+) ч/з функции стоков k_i (x(t)). Будем решать систему (3) методом вариации произвольной постоянной.

Необходимо отметить. Вариация(понятие введенное Ж.Лагранжем) – это термин для обозначения малого смещения независимого переменного или функционала. Метод вариации – это метод исследования экстремальных задач, основанный на малых смещениях аргументов и изучением того, как в зависимости от этого изменяются функционалы.

Таким образом систему (1) интерпретируем следующим образом. Под состоянием вершины графа, отображающего распределительную схему, понимаем величину накопления продуктов соответствующую этой вершине. Тогда один выражает материальный баланс схемы в каждой из ее вершин, при этом величина k_i(x(t)) *x _i (t) – есть сток i-того продукта, а q_i(x(t)) – есть источник i-ой вершины. Отметим, что структура уравнения (1) имеет стандартный вид, дающий возможность для составления уравнений вида (1) для большого числа схем обмена и распределения ресурсов.

Рассмотрим в качестве примера имитационную задачу автоматизированного исследования динамического объекта(на примере гипотетического почвенного комплекса). Смысл задачи состоит в возможности мониторинга компонентного состава исходной графической структуры объекта от «возмущенного» состояния к стабильному образованию.

На первой итерации исходное состояние объекта представляет собой дерево(графическую структуру)вида

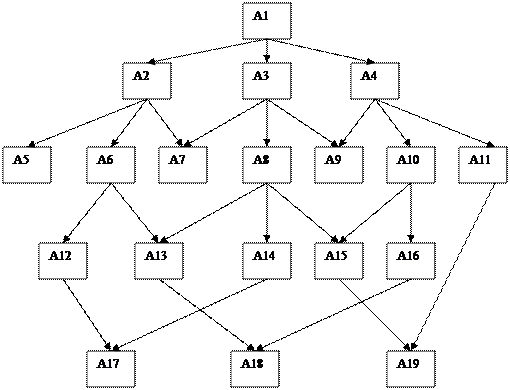
1. А1=А2+А3+А4
2. А2=А5+А6+А7
3. А3=А7+А8+А9
4. А4=А9+А10+А11
5. А6=А12+А13
6. А8=А13+А14+А15
7. А10=А15+А16
8. А11+А15=А19
9. А12+А14=А17
10. А13+А16=А18

Где А1, …, А19 – компонентный состав, à - скорости переходов из одного состояния в другое.

В результате расчета динамики на первой итерации получена новая схем механизма, в которой заметили отсев не стабильных образований

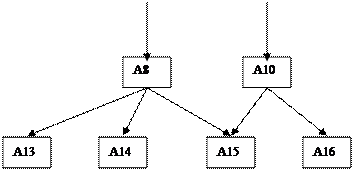На данной итерации схема механизм преобразуется в вид:

1. А1=А2+А3+А4

2. А3=А8

3. А4=А10

4. А8=А13+А14+А15

5. А10=А15+А16

На следующей итерации заметно начало формирования устойчивого комплекса содержащего ряд не стабильных компонентов

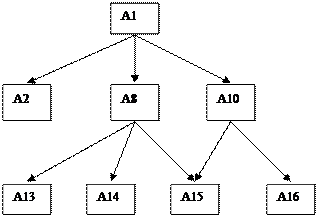1. А1=А2+А8+А10
2. А8=А13+А14+А15
3. А10=А15+А16

Последняя итерация завершает процесс, в результате которого образуется стабильный образ вида:

Черный ящик

По результатам численной реализации покажем график фрагмент образования некоторых стабильных и исчезновение нестабильных компонентов

При изучении динамических объектов, один из примеров которых показан выше, существенно важной является информация по структуре(дереве) объекта, а так же способов ее формализации. Как правило, на начальном этапе исследования специалист имеет более или менее полное представление об исходном состоянии объекта и лишь гипотетическая о его конечной структуре. Что же касается множество промежуточных этапов, то они считаются закрытыми, т.е. специалист имеет дело с «черным ящиком». В то же время, объективно точная информация о промежуточных этапах в совокупности с формальным моделированием промежуточных этапов и процесса в целом позволяет в конечном итоге осуществить реализацию сложных прогнозов и имитационных задач.

Дата добавления: 2014-10-23