
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Математическое обоснование
|
|
|
|
Считаем совокупность элементарных стадий, отражающих с точки зрения специалиста динамику процесса – схемой-механизмом динамического объекта, обозначив ее буквой m, а также то, что уровень профессиональной подготовки специалиста-металлурга таков, что позволяет перечислить все множество М0 – гипотетических схем-механизмов динамики изучаемого процесса.
Общий вид схемы-механизма принимается нами в виде:
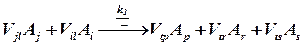 , (1)
, (1) 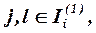
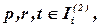
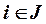 ,
,
где 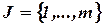 - множество элементарных стадий схемы-механизма;
- множество элементарных стадий схемы-механизма;
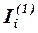 - множество исходных компонент i-го фрагмента;
- множество исходных компонент i-го фрагмента;
 - множество получаемых компонент i-го фрагмента;
- множество получаемых компонент i-го фрагмента;
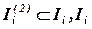 - множество участников i-го фрагмента;
- множество участников i-го фрагмента;
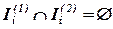 ,
, 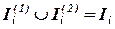 ,
, 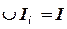 ,
, 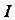 - множество всех участников химического процесса;
- множество всех участников химического процесса;
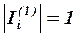 либо
либо 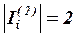 , 1Ј
, 1Ј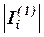 Ј3,
Ј3,
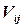 - весовой коэффициент,
- весовой коэффициент, 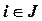 ,
, 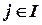 . Считаем, что
. Считаем, что 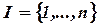 , где n – общее количество составляющих окислительно-восстановительного процесса.
, где n – общее количество составляющих окислительно-восстановительного процесса.
Общее уравнение, определяющее изменение компонент схемы-механизма в единицу времени, представляется в виде:
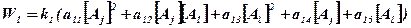 , (2)
, (2)
где 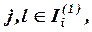
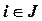 ,
,  либо 1.
либо 1.
Отметим, что приведенная запись используется в большинстве задач классической кинетики. Вспомогательный коэффициент  позволяет рассматривать частные варианты предложенного уравнения, количество которых равно 28.
позволяет рассматривать частные варианты предложенного уравнения, количество которых равно 28.
Дифференциальные уравнения для всех составляющих компонент запишем в виде
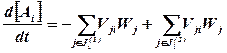 ,
, 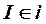 , (3)
, (3)
где 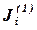 - множество всех элементарных стадий геометрической схемы-механизма, в которых i-я компонента выступает в качестве исходной составляющей,
- множество всех элементарных стадий геометрической схемы-механизма, в которых i-я компонента выступает в качестве исходной составляющей, 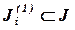 ,
, 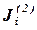 - множество всех элементарных стадий, в которых i-я компонента является конечным продуктом,
- множество всех элементарных стадий, в которых i-я компонента является конечным продуктом, 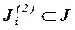 .
.
Таким образом, каждой выбранной схеме-механизму m, можем поставить в соответствие определенный вид выбранной математической модели динамикиg из множества всех возможных моделей М (m), т.е. количество всех участников динамического процесса зависит от схемы механизма m, а именно m=m(m), а g - есть совокупность уравнений вида (2) с конкретным набором вспомогательных коэффициентов, определяющая вид и динамическую структуру математической модели динамического процесса.
Отметим следующий важный момент. Очевидно, что количество составляющих компонент схемы-механизма динамического процесса зависит от m. В то же время ясно и то, что каждый элемент множества М(m) образуется в результате построения определенной комбинации коэффициентов  . Общее количество элементов множества М(m) складывается, таким образом, из совокупности всех видов математической модели. Ранее нами была сделана оценка мощности множества М(m), из которого следует, что количество синтезируемых вариантов представления g из М(m) достигает четвертого порядка.
. Общее количество элементов множества М(m) складывается, таким образом, из совокупности всех видов математической модели. Ранее нами была сделана оценка мощности множества М(m), из которого следует, что количество синтезируемых вариантов представления g из М(m) достигает четвертого порядка.
|
|
|
|
|
Дата добавления: 2014-10-23; Просмотров: 711; Нарушение авторских прав?; Мы поможем в написании вашей работы!