Примеры решения задач. Предложить единую схему решения задач невозможно, однако можно рекомендовать определенную последовательность действий

РЕКОМЕНДАЦИИ ПО РЕШЕНИЮ ЗАДАЧ

Предложить единую схему решения задач невозможно, однако можно рекомендовать определенную последовательность действий. Приступая к решению задач по какому-либо разделу, необходимо ознакомиться с конкретными физическими понятиями и соотношениями этого раздела, разобрать приведенные примеры решения задач. При самостоятельном решении задач целесообразно придерживаться следующей схемы:

1) по условию задачи представьте себе физическое явление, о котором идет речь, сделайте краткую запись условия, выразив исходные данные в единицах СИ;

2) сделайте, если это необходимо, рисунок, поясняющий описываемый в задаче процесс;

3) напишите уравнение или систему уравнений, отображающих физический процесс;

4) преобразуйте уравнения так, чтобы в них входили лишь исходные данные и табличные величины;

5) решите задачу в общем виде;

6) произведите вычисления и оцените реальность числового ответа.

Пример 1. Точечный заряд q =25 нКл находится в ноле, созданном прямым бесконечным цилиндром радиусом R= 1 см, равномерно заряженным с поверхностной плотностью s=2 мкКл/м². Определить силу, действующую на заряд, помещенный от оси цилиндра на расстоянии r =10 см.

Решение. Сила, действующая на заряд q, находящийся в поле

F=qE,

где Е — напряженность поля в точке, в которой находится заряд q.

Как известно, напряженность поля бесконечно длинного равномерно заряженного цилиндра

E =,

где t — линейная плотность заряда.

Выразим линейную плотность t через поверхностную плотность s. Для этого выделим элемент цилиндра длиной l и выразим находящийся на нем заряд q₁ двумя способами

q₁=sS=s2pRl и q ₁ =t l

Приравняв правые части этих равенств, получим t l =2p Rls. После сокращения на l найдем t=2p Rs. С учетом этого формула напряженности поля примет вид E=Rs/(e₀r). Подставив это выражение Е в формулу силы, действующей на заряд q, находящийся в поле, найдем искомую силу

F=qsR/(e₀r)

Так как R и r входят в формулу в виде отношения, то они могут быть выражены в любых, но только одинаковых единицах.

Выполнив вычисления по последней формуле, найдем

F =25×10^-9×2×10^-6×10^-2/(8,85×10^-12×10×10^-2)H==565×10^-6H=565мкH.

Направление силы 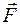совпадает с направлением вектора напряженности 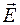, а последний в силу симметрии (цилиндр бесконечно длинный) направлен перпендикулярно цилиндру.

Пример 2. Положительные заряды q₁ =3 мкКл и q₂ =20 нКл находятся в вакууме на расстоянии r₁ =l,5 м друг от друга. Определить работу A, которую надо совершить, чтобы сблизить заряды до расстояния r₂ =1 м.

Решение. Положим, что первый заряд q₁ остается неподвижным, а второй q₂ под действием внешних сил перемещается в поле, созданном зарядом q₁, приближаясь к нему с расстояния r₁ =t,5 м до r₂ =1 м.

Работа А' внешней силы по перемещению заряда q из однойточки поля с потенциалом j ₁ в другую, потенциал которой j ₂, равна по модулю и противоположна по знаку работе А сил поля по перемещению заряда между теми же точками

А '= — А

Работа А сил поля по перемещению заряда A = q (j ₁ —j ₂). Тогда работа А' внешних сил может быть записана в виде

A' = – q (j ₁ —j ₂)= q (j ₂ — j₁)

Потенциалы точек начала и конца пути выразятся формулами

,

Подставляя выражения j ₁ и j ₂ в формулу работы внешних сил и учитывая, что для данного случая переносимый заряд q = q₂, получим

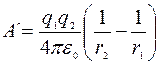
Если учесть, что 1/(4pe ₀)=9×10⁹ м/Ф, то после подстановки значений величин в последнюю формулу работы внешних сил и вычисления найдем

A '=180 мкДж

Пример 3. Определить электрическую емкость С плоского конденсатора с двумя слоями диэлектриков: фарфора толщиной d ₁ = 2 мм и эбонита толщиной d ₂ = 1,5 мм, если площадь S пластин равна 100 см².

Решение. Емкость конденсатора, по определению

,

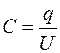где q - заряд на пластинах конденсатора; U - разность потенциалов пластин. Заменив в этом равенстве общую разность потенциалов U конденсатора суммой U ₁ +U ₂напряжений на слоях диэлектриков, получим

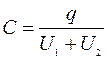
Принимая во внимание, что

, и ,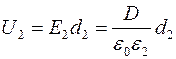

тогда формулу для емкости конденсатора можно переписать в виде

,

где σ - поверхностная плотность заряда на пластинах; Е ₁ и Е ₂ - напряженности поля в первом и втором слоях диэлектрика соответственно; D - электрическое смещение поля в диэлектриках.

Умножив числитель и знаменатель последнего равенства на ε₀ и учтя, что D=σ, получим окончательную формулу для определения емкости плоского конденсатора

Сделав подстановку числовых значений d ₁, d ₂, e₁, e₂, e₀, и S в последнюю формулу, найдем электрическую емкость С плоского конденсатора с двумя слоями диэлектриков

Пример 4. Плоский конденсатор заряжен до разности потенциалов U = 1 кВ. Расстояние d между пластинами равно 1 см. Диэлектрик - стекло. Определить объемную плотность энергии поля конденсатора.

Решение. Объемная плотность энергии поля конденсатора

,

где W - энергия поля конденсатора; V- объем, занимаемый полем, т. е. объем пространства, заключенного между пластинами конденсатора.

Энергия поля конденсатора определяется по формуле

,

где U - разность потенциалов, до которой заряжены пластины конденсатора; С - его электроемкость. Но

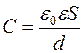и

Подставив выражение для электроемкости в формулу энергии поля конденсатора и затем выражения этой энергии и объема в формулу для объемной плотности энергии поля конденсатора, получим

Подставим значения величин в последнюю формулу и произведя вычисления, найдем

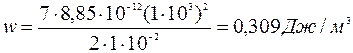
Пример 5. Определить заряд q, прошедший по проводу с сопротивлением R= 3Ом при равномерном нарастании напряжения на концах провода от U ₀ = 2В до U = 4В в течение t= 20с.

Решение. Так как сила тока в проводе изменяется, то воспользоваться для подсчета заряда формулой q=It нельзя. Поэтому возьмем дифференциал заряда d q=I d t и проинтегрируем

Выразив силу тока по закону Ома, получим

Напряжение U в данном случае изменяется со временем. В силу равномерности нарастания оно может быть выражено формулой

U= U ₀ +kt,

где k - коэффициент пропорциональности. Подставив это выражение U в формулу вычисления для заряда, найдем

Проинтегрировав, получим

Значение коэффициента пропорциональности k найдем из формулы U= U ₀ +kt, если заметим, что при t= 20 с U= 4В, тогда

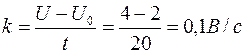
Подставив значения величин вформулу для вычисления заряда, получим

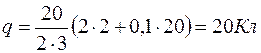
Пример 7. В цепь источника постоянного тока с ЭДС ε= 6В включен резистор сопротивлением R= 80Ом. Определить: 1)плотность тока в соединительных проводах площадью поперечного сечения S= 2мм²; 2)число N электронов, проходящих через сечение проводов за время t= 1 с. Сопротивлением источника тока и соединительных проводов пренебречь.

Решение. 1.Плотность тока по определению есть отношение силы тока I к площади поперечного сечения провода

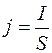
Силу тока в этой формуле выразим по закону Ома

,

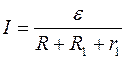где R - сопротивление резистора; R ₁ - сопротивление соединительных проводов; r ₁- внутреннее сопротивление источника тока.

Пренебрегая сопротивлениями R _lи r ₁из формулы закона Ома, получим

Подставив это выражение силы тока в формулу плотности тока, получим

Произведя вычисления по этой формуле, получим

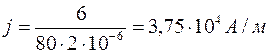
2.Число электронов, проходящих за время t через поперечное сечение, найдем, разделив заряд q, протекающий за это время через сечение, на элементарный заряд

,

или с учетом того, что q=It и I=ε/R

Подставим в эту формулу числовые значения величин и вычислим

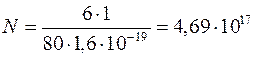электронов

Пример 7. На проволочный виток радиусом r =10см, помещенный между полюсами магнита, действует максимальный механический момент М _max=6,5 мкНм. Сила тока I в витке равна 2 А. Определить магнитную индукцию В поля между полюсами магнита. Действием магнитного поля Земли пренебречь.

Решение. Индукцию В магнитного поля можно определить из выражения механического момента, действующего на виток с током в магнитном поле

Если учесть, что максимальное значение механический момент принимает при α=π/2(sin α=l), а также что p_m=IS, то формула механического момента примет вид

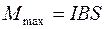
Отсюда, учитывая, что S= π r², находим

Произведя вычисления по последней формуле, найдем

Пример 8. Определить индукцию В и напряженность Н магнитного поля на оси тороида без сердечника, по обмотке которого, содержащей N =200 витков, идет ток I =5 А. Внешний диаметр d ₁тороида равен 30 см, внутренний d ₂ = 20 см.

Решение. Для определения напряженности магнитного поля внутри тороида вычислим циркуляцию вектора 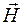вдоль линии магнитной индукции поля

Из условия симметрии следует, что линии магнитной индукции тороида представляют собой окружности, и что во всех точках этой линии напряженности одинаковы. Поэтому в выражении циркуляции напряженность Н можно вынести за знак интеграла, а интегрирование проводить в пределах от нуля до 2 p r, где r — радиус окружности, совпадающей с линией индукции, вдоль которой вычисляется циркуляция, т. e.

С другой стороны, в соответствии с законом полного тока циркуляция вектора напряженности магнитного поля равна сумме токов, охватываемых контуром, вдоль которого вычисляется циркуляция

Приравняв правые части последних двух равенств, получим

Линия, проходящая вдоль тороида, охватывает число токов, равное числу витков тороида. Сила тока во всех витках одинакова. Поэтому последнее равенство примет вид 2prH=NI, откуда

Для средней линии тороида r =1/2(R ₁ R ₂)=1/4(d ₁+ d ₂). Подставив это выражение r в формулу напряженности, найдем

Подставив значения величин в эту формулу, получим

Магнитная индукция В ₀в вакууме связана с напряженностью поля соотношением B ₀ = m₀ H. Следовательно

Подставив значения величин в последнюю формулу, получим

Пример 9. Электрон, пройдя ускоряющую разность потенциалов U =400 В, попал воднородное магнитное поле с индукцией B =1,5 мТл. Определить: 1) радиус R кривизны траектории; 2)частоту п вращения электрона вмагнитном поле. Вектор скорости электрона перпендикулярен линиям индукции.

Решение. 1.Радиус кривизны траектории электрона определим исходя из следующих соображений: на движущийся в магнитном поле электрон действует сила Лоренца F. (Действием силы тяжести можно пренебречь.) Вектор силы Лоренца перпендикулярен вектору скорости и, следовательно, по второму закону Ньютона, сообщает электрону нормальное ускорение а_n

F=ma_n

Подставив сюда выражения силы Лоренца F и нормального ускорения а_n, получим

,

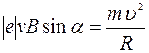где е, v, т — заряд, скорость, масса электрона; В — индукция магнитного поля; R — радиус кривизны траектории; a — угол между направлениями векторов скорости 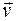и магнитной индукции 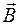(в нашем случае 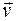^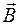и a = 90°, следовательно sin a =l).

Из формулы силы Лоренца найдем радиус кривизны траектории

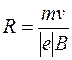
Входящий в последнюю формулу импульс mv выразим через кинетическую энергию W_K электрона

Но кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U, определяется равенством W_K = | e | U. Подставив это выражение W_K в формулу импульса, получим

Тогда выражение для радиуса кривизны траектоии приобретает вид

Подставив числовые значения величин в последнюю формулу, получим

2.Для определения частоты вращения воспользуемся формулой связывающей частоту со скоростью и радиусом кривизны траектории

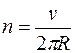
Подставив формулу радиуса кривизны траектории 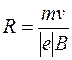в последнюю формулу, получим

Произведя вычисления по последней формуле, найдем

Пример 10. В однородном магнитном поле с индукцией B =0,1 Тл равномерно вращается рамка, содержащая N= 1000 витков, с частотой n=l0 c ^-1. Площадь S рамки равна 150 см². Определить мгновенное значение ЭДС , соответствующее углу поворота рамки 30°.

Решение. Мгновенное значение ЭДС индукции , определяется основным уравнением электромагнитной индукции Фарадея — Максвелла

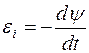
Потокосцепление Y = NФ, где N — число витков, пронизываемых магнитным потоком Ф. Подставив выражение Y в формулу мгновенного значения ЭДС индукции, получим

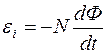
При вращении рамки магнитный поток Ф, пронизывающий рамку в момент времени t, изменяется по закону Ф=ВS cosw t, где В — магнитная индукция; S — площадь рамки; w — угловая частота. Подставив в последнюю формулу выражение магнитного потока Ф и продифференцировав по времени, найдем мгновенное значение ЭДС индукции

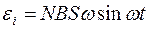
Угловая частота w связана с частотой п вращения соотношением w=2p п. Подставив выражение угловой частоты в формулу ЭДС индукции и заменив w t на угол a, получим

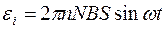
Произведя вычисления по последней формуле, получим

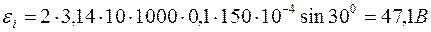
Пример 11. На стержень из немагнитного материала длиной l =50 см намотан в один слой провод так, что на каждый сантиметр длины стержня приходится 20 витков. Определить энергию W магнитного поля внутри соленоида, если сила тока I в обмотке равна 0,5 А. Площадь S сечения стержня равна 2 см².

Решение. Энергия магнитного поля соленоида с индуктивностью L, по обмотке которого течет ток I, выражается формулой

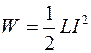
Индуктивность соленоида в случае немагнитного сердечника зависит только от числа витков на единицу длины и от объема V сердечника: L=μ₀n²V, где μ₀ —магнитная постоянная. Подставив выражение индуктивности L в формулу энергии магнитного поля, получим

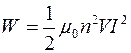
Учтя, что V=lS, тогда запишем формулу энергии магнитного поля следующим образом

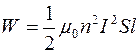
Сделав вычисления по последней формуле, найдем

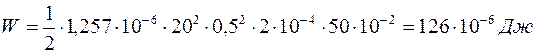
Дата добавления: 2014-10-23