
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теоретическая часть. Лабораторная работа № 3. Исследование электрической схемы замещения магнитной цепи
|
|
|
|
Лабораторная работа № 3. Исследование электрической схемы замещения магнитной цепи
ЦЕЛЬ РАБОТЫ: ознакомиться с методом математического моделирования магнитных цепей в электромеханических устройствах с использованием электрических схем замещения.
Электромагнитное поле в общем случае описывается системой уравнений Максвелла, которая в дифференциальной форме выглядит следующим образом:
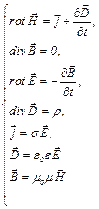 (3.1)
(3.1)
Здесь 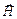 – вектор напряженности магнитного поля, А/м;
– вектор напряженности магнитного поля, А/м; 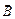 – вектор индукции магнитного поля, Тл;
– вектор индукции магнитного поля, Тл; 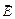 – вектор напряженности электрического поля, В/м;
– вектор напряженности электрического поля, В/м; 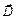 – вектор электростатической индукции, Кл/м2;
– вектор электростатической индукции, Кл/м2;  – вектор плотности тока; σ – удельная проводимость; ε – диэлектрическая проницаемость среды; ε0 – электрическая постоянная, Ф/м; μ – магнитная проницаемость среды; μ0 – магнитная проницаемость вакуума, Гн/м. Для линейной задачи σ = const, ε = const, μ = const.
– вектор плотности тока; σ – удельная проводимость; ε – диэлектрическая проницаемость среды; ε0 – электрическая постоянная, Ф/м; μ – магнитная проницаемость среды; μ0 – магнитная проницаемость вакуума, Гн/м. Для линейной задачи σ = const, ε = const, μ = const.
Статическое магнитное поле является частным случаем электромагнитного поля и описывается системой уравнений
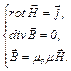 (3.2)
(3.2)
В интегральной форме данная система уравнений принимает вид
 (3.3)
(3.3)
Здесь первое уравнение представляет собой закон полного тока: циркуляция вектора 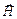 по замкнутому контуру l равна полному току, охваченному данным контуром, который может вычисляться как интеграл от плотности тока
по замкнутому контуру l равна полному току, охваченному данным контуром, который может вычисляться как интеграл от плотности тока  по площади контура S или как сумма токов Ij в N проводниках, охваченных контуром.
по площади контура S или как сумма токов Ij в N проводниках, охваченных контуром.
Во многих случаях в электромеханических системах закон полного тока может быть представлен в форме
 , (3.4)
, (3.4)
где Hi – касательная проекция вектора напряженности магнитного поля на участке длиной li; I – ток в обмотке с количеством витков W; F – намагничивающая сила обмотки.
Проведем преобразования:
 . (3.5)
. (3.5)
Получаем закон Ома для магнитной цепи:
 , (3.6)
, (3.6)
где F – магнитодвижущая сила магнитной цепи;
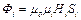 – магнитный поток на i-м участке магнитной цепи;
– магнитный поток на i-м участке магнитной цепи;
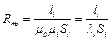 – магнитное сопротивление i-го участка магнитной цепи; λ = μ0μ – удельная магнитная проводимость участка магнитной цепи; l – длина участка магнитной цепи; S – сечение участка магнитной цепи.
– магнитное сопротивление i-го участка магнитной цепи; λ = μ0μ – удельная магнитная проводимость участка магнитной цепи; l – длина участка магнитной цепи; S – сечение участка магнитной цепи.
Следует отметить, что магнитное сопротивление вычисляется по формуле, изоморфной с формулой электрического сопротивления.
Выясним, при каких условиях электрическая и магнитная цепи подобны. Для этого воспользуемся первой теоремой подобия. Для определения условий, критериев и масштабов подобия выполним определенные действия в следующем порядке:
1. Определим соответствие величин оригинала и модели:
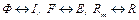 . (3.7)
. (3.7)
2. Введем масштабы подобия:
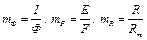 . (3.8)
. (3.8)
3. Приведем уравнения тепловых и электрических процессов к безразмерному виду:
 ; (3.9)
; (3.9)
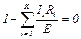 . (3.10)
. (3.10)
4. Подставим в уравнение (3.10) величины из уравнения (3.9) с соответствующими масштабными коэффициентами:
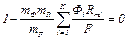 . (3.11)
. (3.11)
5. Уравнение (3.9) тождественно уравнению (3.11) при выполнении условия
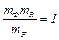 .. (3.12)
.. (3.12)
6. На основании (3.12) получим выражение критерия подобия
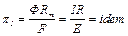 . (3.13)
. (3.13)
7. Проведем анализ размерностей величин, входящих в уравнение оригинала (3.9):
 (3.14)
(3.14)
Видим, что размерности всех шести величин могут быть построены из двух основных размерностей: Вб, А. Это значит, что из трех масштабов подобия два масштаба являются независимыми, то есть их значения можно выбрать произвольным образом, а один – является зависимым. В качестве зависимого удобнее всего выбрать масштаб 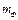 . Остальным масштабам mR и mF можно присвоить любые произвольные значения. В целях упрощения модели величины сопротивлений и МДС можно выбрать равными соответствующим величинам тепловых сопротивлений и ЭДС, то есть mR = mF = 1.
. Остальным масштабам mR и mF можно присвоить любые произвольные значения. В целях упрощения модели величины сопротивлений и МДС можно выбрать равными соответствующим величинам тепловых сопротивлений и ЭДС, то есть mR = mF = 1.
Зависимый масштаб должен быть рассчитан из (3.12):
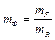 . (3.15)
. (3.15)
Следует отметить, что подобие магнитной и электрической цепей распространяется и на случай разветвленных магнитных цепей, где в качестве ветвей магнитной цепи выступают участки магнитопровода.
В простейшем случае при построении электрической схемы замещения магнитной цепи исследуемый магнитопровод разбивается вдоль силовой линии магнитного поля на участки с разным значением магнитного сопротивления (рис. 3.1, а). Каждый участок заменяется магнитным сопротивлением Rm, которому в соответствие ставится электрическое сопротивление R, связанное с магнитным сопротивлением соотношением (3.10). Обмотке с намагничивающей силой F в электрической схеме замещения соответствует ЭДС E (рис. 3.1, б).
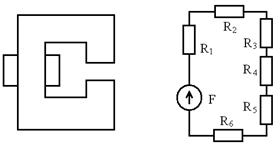
Рис. 3.1. Магнитная система реактора (а) и ее упрощенная электрическая схема замещения (б)
В более точных моделях массивные участки магнитопровода моделируются электрической сеткой, построенной из электрических сопротивлений, каждый из которых соответствует определенному участку 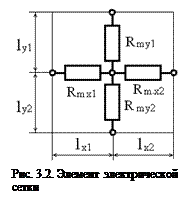 магнитопровода и определенному направлению магнитного потока. Наибольшее распространение получили сетки с прямоугольными ячейками (рис. 3.2). Каждое электрическое сопротивление соответствует магнитному сопротивлению i-го прямоугольного участка длиной Δli, сечением ΔSi, вычисляемому как
магнитопровода и определенному направлению магнитного потока. Наибольшее распространение получили сетки с прямоугольными ячейками (рис. 3.2). Каждое электрическое сопротивление соответствует магнитному сопротивлению i-го прямоугольного участка длиной Δli, сечением ΔSi, вычисляемому как 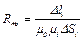 . Например, сопротивления, изображенные на рис. 3.2, рассчитываются как
. Например, сопротивления, изображенные на рис. 3.2, рассчитываются как
 ,
, 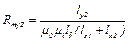 ,
,
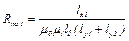 ,
, 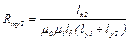 , (3.16)
, (3.16)
где lδ – расчетная длина зазора (машины) в осевом направлении.

Магнитодвижущая сила обмотки в этом случае распределяется равномерно по вертикальным участкам сердечника полюса, охваченного катушкой возбуждения.
Уточненная электрическая схема замещения магнитной цепи машины постоянного тока (МПТ) изображена на рис. 3.3.
В результате расчета электрической схемы замещения, изображенной на рис. 3.3, получаем токи в сопротивлениях, которые пересчитываются в магнитные потоки на соответствующем участке магнитопровода:
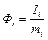 . (3.17)
. (3.17)
Величину индукции можно рассчитать на участках, соответствующих магнитным сопротивлениям. При этом на сопротивлениях с индексом x (на рис. 3.2 – это Rmx1 и Rmx1) рассчитываются составляющие индукции по оси x и y:
 и
и  ,
,
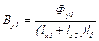 и
и  , (3.18)
, (3.18)
где Фxi, Фyi – величина магнитного потока в i-м магнитном сопротивлении.
Значения электрических потенциалов в узлах сетки пересчитываются в значения скалярного магнитного потенциала:
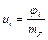 . (3.20)
. (3.20)
|
|
|
|
|
Дата добавления: 2014-10-23; Просмотров: 424; Нарушение авторских прав?; Мы поможем в написании вашей работы!