Теоретическая часть

Лабораторная работа № 2. Исследование электрической схемы замещения тепловой цепи асинхронного двигателя

ЦЕЛЬ РАБОТЫ: ознакомиться с методом математического моделирования тепловых процессов в электромеханических устройствах с использованием электрических схем замещения.

В активных и конструктивных элементах электрических машин выделяются потери, природа и характер которых определяются основными и добавочными процессами. Температурные поля в общем случае изменяются по каждой из трех пространственных координат и не остаются постоянными с течением времени. Теплообмен в электрических машинах происходит путем теплопроводности, конвективного теплообмена и излучения.

Согласно основному закону теплопроводности, количество тепла Q, передаваемого за единицу времени через произвольную изотермическую поверхность S, прямо пропорционально градиенту температуры grad 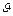в направлении теплового потока:

, (2.1)

где 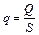– плотность теплового потока, Вт/м²; λ – удельная теплопроводность материала, Вт/(м^.оС). Единицы измерения [ Q ] = Вт, [ S ] = м², [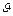] = ^оС, [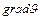] = ^оС/м.

Удельная теплопроводность характеризует способность вещества проводить тепло, определяется физическими свойствами вещества и зависит от его состава, температуры и давления (для газообразных веществ). Знак минус в (2.1) показывает, что тепловой поток распространяется от точки тела с большей температурой к точке с меньшей температурой.

При одномерном распространении тепла имеем

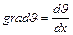, (2.2)

где х – направление распространения тепла.

Таким образом, имеем следующее выражение:

. (2.3)

Если же рассматривать однородную стенку толщиной b_c при отсутствии в ней источников тепла, то мы придем к следующему выражению:

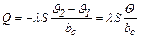, (2.4)

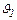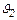где и – температуры на границах стенки вдоль линии распространения тепла; 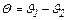– перепад температур на границах стенки.

Конвективный теплообмен между поверхностью твердого тела и газообразной средой описывается экспериментальным законом Ньютона – Рихмана, связывающим плотность теплового потока на поверхности q с температурами поверхности 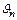и среды :

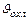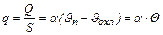, (2.5)

где α – коэффициент теплоотдачи поверхности, Вт/(м^{2. о}С), характеризующий интенсивность теплообмена; 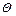– превышение температуры охлаждаемой поверхности над температурой охлаждающей среды, ^оС.

Соответственно, перепад температуры между поверхностью и охлаждающей средой составит

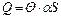. (2.6)

Из приведенных выше выражений видно, что тепло, передаваемое через стенку или с поверхности, прямо пропорционально перепаду температур.

Введем понятие теплового сопротивления R_т, определяющего перепад температуры, аналогично электрическому сопротивлению R_э, вызывающему соответствующее падение напряжения в цепи. Для однородной стенки

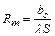, (2.7)

для теплоотдачи с поверхности

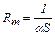. (2.8)

Тепловое сопротивление измеряется в ^оС/Вт.

С учетом (2.7) и (2.8) выражения (2.4) и (2.6) получают форму закона Ома для участка тепловой цепи:

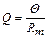. (2.9)

Один из возможных вариантов тепловой цепи асинхронного двигателя (АД) защищенного исполнения представлен на рис. 2.1.

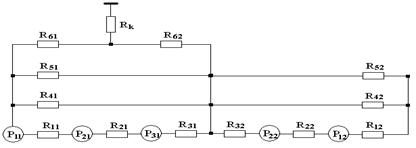
Рис. 2.1. Тепловая цепь асинхронного двигателя

Для составления тепловой цепи всю тепловую систему машины с непрерывно распределенными тепловыми источниками и тепловыми параметрами заменяют эквивалентной схемой, составленной из тепловых сопротивлений и источников теплопотерь.

Статор АД в тепловом отношении можно разбить на три условно однородные части, являющиеся источником тепла:

· стальной сердечник с потерями Р₁₁;

· пазовую часть обмотки статора с источниками теплопотерь Р₂₁;

· лобовые части обмотки статора с источниками теплопотерь Р₃₁.

В роторе АД в номинальном режиме есть два источника тепла:

· пазовая часть обмотки ротора с источниками теплопотерь Р₁₂;

· лобовые части обмотки ротора с источниками теплопотерь Р₂₂.

Принимаем следующие пути рассеяния тепловых потоков:

1) тепловой поток Q₁₁ от пазовой части обмотки статора к стенкам зубцов и ярму сердечника статора через пазовую изоляцию с тепловым сопротивлением

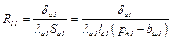, (2.10)

где δ_и1 – толщина пазовой изоляции обмотки статора; λ_и1 – удельная теплопроводность пазовой изоляции обмотки статора; 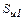– площадь пазовой изоляции во всех пазах статора; l_с1 – длина пакета статора; p_п1 – периметр паза статора; b_ш1 – ширина шлица паза статора;

2) тепловой поток Q₂₁ от пазовых частей обмотки статора к лобовым частям вдоль проводников с тепловым сопротивлением

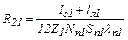, (2.11)

где l_с1 – длина пакета статора; l_л1 – длина лобовой части обмотки статора; Z₁ – количество пазов статора; N_п1 – число проводников в пазу статора; S_п1 – сечение проводника обмотки статора; λ_п1 – удельная теплоемкость материала проводника; коэффициент 1/12 учитывает равномерное распределение теплопотерь по длине проводника;

3) тепловой поток Q₃₁ от лобовых частей обмотки статора к охлаждающему воздуху через тепловое сопротивление

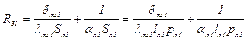, (2.12)

где δ_ли1 – толщина изоляции лобовых частей; λ_ли1 – удельная теплопроводность изоляции лобовых частей; 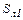– площадь теплоотдачи лобовых частей; α_л1 – коэффициент теплоотдачи лобовых частей; l_л1 – длина лобовой части обмотки статора; p_л1 – периметр лобовой части обмотки статора;

4) тепловой поток Q₄₁ с торцевой поверхности сердечника статора к охлаждающему воздуху через тепловое сопротивление

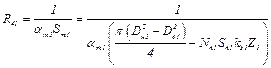, (2.13)

где 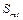– площадь теплоотдачи с торцевой поверхности статора; α_т1 – коэффициент теплоотдачи с торцевой поверхности статора; D_н1 – наружный диаметр пакета статора; D_в1 – внутренний диаметр пакета статора; N_п1 – число проводников в пазу статора; S_п1 – сечение проводника обмотки статора; k_з1 – коэффициент заполнения паза статора; Z₁ – количество пазов статора;

5) тепловой поток Q₅₁ с поверхности сердечника статора к воздуху зазора через тепловое сопротивление

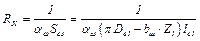, (2.14)

где 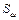– площадь расточки статора за вычетом площади шлицов; α_сз – коэффициент теплоотдачи с внутренней поверхности статора; D_в1 – внутренний диаметр статора; b_ш1 – ширина шлица паза статора; l_с1 – длина пакета статора; Z₁ – количество пазов статора;

6) тепловой поток Q₆₁ с поверхности статора к корпусу через тепловое сопротивление

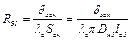, (2.15)

где δ_зск – толщина зазора между статором и корпусом; λ_в – удельная теплопроводность воздуха; 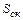– площадь контакта между статором и корпусом; D_н1 – наружный диаметр пакета статора; l_с1 – длина пакета статора;

7) тепловой поток Q₁₂ от пазовой части обмотки ротора к стенкам зубцов и ярму сердечника ротора через пазовую изоляцию с тепловым сопротивлением

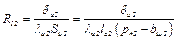, (2.16)

где δ_и2 – толщина пазовой изоляции обмотки ротора; λ_и2 – удельная теплопроводность пазовой изоляции обмотки ротора; 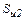– площадь пазовой изоляции во всех пазах ротора; l_с2 – длина пакета ротора; p_п2 – периметр паза ротора; b_ш2 – ширина шлица паза ротора;

8) тепловой поток Q₂₂ от пазовых частей обмотки ротора к лобовым частям вдоль проводников с тепловым сопротивлением

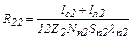, (2.17)

где l_с2 – длина пакета ротора; l_л2 – длина лобовой части обмотки ротора; Z₂ – количество пазов ротора; N_п2 – число проводников в пазу ротора; S_п2 – сечение проводника обмотки ротора; λ_п2 – удельная теплопроводность материала проводника; коэффициент 1/12 учитывает равномерное распределение теплопотерь по длине проводника;

9) тепловой поток Q₃₂ от лобовых частей обмотки к охлаждающему воздуху через тепловое сопротивление

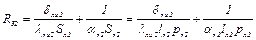, (2.18)

где δ_ли2 – толщина изоляции лобовых частей; λ_ли2 – удельная теплопроводность изоляции лобовых частей; 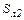– площадь теплоотдачи лобовых частей; α_л2 – коэффициент теплоотдачи с поверхности лобовых частей обмотки ротора; l_л2 – длина лобовой части обмотки ротора; p_л2 – периметр лобовой части обмотки ротора;

10) тепловой поток Q₄₂ с торцевой поверхности сердечника ротора к охлаждающему воздуху через тепловое сопротивление

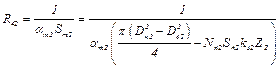, (2.19)

где 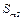– площадь теплоотдачи с торцевой поверхности ротора; α_т2 – коэффициент теплоотдачи с торцевой поверхности ротора; D_н2 – наружный диаметр пакета ротора; D_в2 – внутренний диаметр пакета ротора; N_п2 – число проводников в пазу ротора; S_п2 – сечение проводника обмотки ротора; k_з2 – коэффициент заполнения паза ротора; Z₂ – количество пазов ротора;

11) тепловой поток Q₅₂ с поверхности сердечника ротора к воздуху зазора через тепловое сопротивление

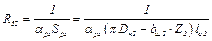, (2.20)

где – площадь расточки ротора за вычетом площади шлицов; α_рз – коэффициент теплоотдачи с внешней поверхности ротора; D_н2 – наружный диаметр пакета ротора; b_ш2 – ширина шлица паза ротора; l_с2 – длина пакета ротора; Z₂ – количество пазов ротора;

12) тепловой поток Q₆₂ от воздуха внутри машины к корпусу через тепловое сопротивление

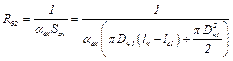, (2.21)

где 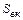– площадь контакта воздуха внутри машины с корпусом; α_вк – коэффициент теплоотдачи от воздуха к корпусу; l_к – длина корпуса машины; l_с1 – длина пакета статора; D_н1 – наружный диаметр пакета статора;

13) тепловой поток Q_к с поверхности корпуса к охлаждающему воздуху за пределами машины через тепловое сопротивление

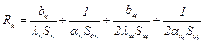, (2.22)

где b_к – толщина корпуса; b_щ – толщина подшипникового щита; λ_к – удельная теплопроводность корпуса; λ_щ – удельная теплопроводность подшипникового щита; α_к – коэффициент теплоотдачи с поверхности корпуса; α_щ – коэффициент теплоотдачи с поверхности подшипникового щита;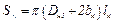– площадь цилиндрической поверхности корпуса; 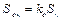– площадь теплоотдачи с поверхности корпуса с учетом оребрения; – площадь теплоотдачи с поверхности подшипникового щита; l_к – длина корпуса машины; D_н1 – наружный диаметр пакета статора; k_о – коэффициент увеличения периметра корпуса за счет оребрения.

Нагрев каждого элемента тепловой цепи происходит с определенной инерцией. За инертность процессов в тепловой цепи отвечает теплоемкость. Теплоемкости отдельных элементов тепловой цепи вычисляются следующим образом:

1) теплоемкость стали статора

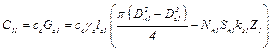, (2.23)

где с_с – удельная теплоемкость стали; G_с1 – вес стали статора; γ_с – удельный вес стали; D_н1 – наружный диаметр пакета статора; D_в1 – внутренний диаметр пакета статора; N_п1 – число проводников в пазу статора; S_п1 – сечение проводника обмотки статора; k_з1 – коэффициент заполнения паза статора; Z₁ – количество пазов статора;

2) теплоемкость проводников в пазу статора

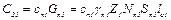, (2.24)

где с_п1 – удельная теплоемкость проводников обмотки статора; G_п1 – вес проводников в пазах статора; γ_п1 – удельный вес материала проводников обмотки статора; N_п1 – число проводников в пазу статора; S_п1 – сечение проводника обмотки статора; Z₁ – количество пазов статора; l_с1 – длина пакета статора;

3) теплоемкость проводников в лобовых частях обмотки статора

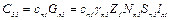, (2.25)

где с_п1 – удельная теплоемкость проводников обмотки статора; G_л1 – вес проводников в лобовых частях обмотки статора; γ_п1 – удельный вес материала проводников обмотки статора; N_п1 – число проводников в пазу статора; S_п1 – сечение проводника обмотки статора; Z₁ – количество пазов статора; l_л1 – длина лобовой части обмотки статора;

4) теплоемкость проводников в пазу ротора

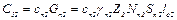, (2.26)

где с_п2 – удельная теплоемкость проводников обмотки ротора; G_п2 – вес проводников в пазах ротора; γ_п2 – удельный вес материала проводников обмотки ротора; N_п2 – число проводников в пазу ротора; S_п2 – сечение проводника обмотки ротора; Z₂ – количество пазов ротора; l_с2 – длина пакета ротора;

5) теплоемкость проводников в лобовых частях обмотки ротора

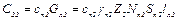, (2.27)

где с_п2 – удельная теплоемкость проводников обмотки ротора; G_л2 – вес проводников в лобовых частях обмотки ротора; γ_п2 – удельный вес материала проводников обмотки ротора; N_п2 – число проводников в пазу ротора; S_п2 – сечение проводника обмотки ротора; Z₂ – количество пазов ротора; l_л2 – длина лобовой части обмотки ротора;

6) теплоемкость стали ротора

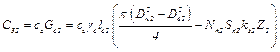, (2.28)

где с_с – удельная теплоемкость стали; G_с1 – вес стали ротора; γ_с – удельный вес стали; l_с2 – длина пакета ротора; D_н1 – наружный диаметр пакета ротора; D_в1 – внутренний диаметр пакета ротора; N_п1 – число проводников в пазу ротора; S_п1 – сечение проводника обмотки ротора; k_з1 – коэффициент заполнения паза ротора; Z₁ – количество пазов ротора;

7) теплоемкость воздуха внутри машины

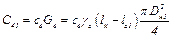, (2.29)

где с_в – удельная теплоемкость воздуха; G_в – вес воздуха внутри машины; γ_с – удельный вес воздуха; l_с1 – длина корпуса; l_с1 – длина пакета статора; D_н1 – наружный диаметр пакета ротора;

8) теплоемкость корпуса и подшипниковых щитов

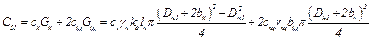, (2.30)

где с_к – удельная теплоемкость вещества корпуса; G_в – вес корпуса; с_щ – удельная теплоемкость вещества подшипниковых щитов; G_щ – вес подшипникового щита; γ_к – удельный вес вещества корпуса; γ_щ – удельный вес вещества подшипникового щита; l_к – длина корпуса машины; D_н1 – наружный диаметр пакета статора; k_о – коэффициент увеличения периметра корпуса за счет оребрения; b_к – толщина корпуса; b_щ – толщина подшипникового щита.

При неизменных потерях Q, выделяемых в теле, дифференциальное уравнение нагрева однородного тела имеет вид

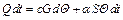, (2.31)

где t – время, с; с – удельная теплоемкость, Дж/(кг ^{. о}С); G – вес тела, кг.

Представим данное уравнение в виде

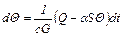, (2.32)

или

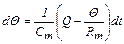, (2.33)

где 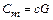– теплоемкость однородного тела, Дж/(^оС).

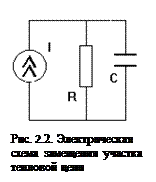
Это уравнение изоморфно с уравнением электрической цепи, изображенной на рис. 2.2:

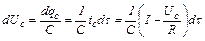, (2.34)

где U_c – напряжение на конденсаторе, В; q_c – заряд конденсатора, Кл; С – емкость конденсатора, Ф; i_c – ток, протекающей через конденсатор, А; τ – время, с; I – ток в ветви с источником тока, А; R – сопротивление, Ом.

Следует отметить также, что форма записи выражений для расчета тепловых сопротивлений совпадает с формой записи выражения для электрического сопротивления:

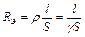, (2.35)

где ρ – удельное сопротивление проводника; γ – удельная проводимость проводника; l – длина проводника; S – сечение проводника.

Таким образом, есть два процесса, описываемые изоморфными уравнениями. Следовательно, можно построить электрическую схему замещения тепловых процессов. Электрическая схема замещения тепловой цепи АД, изображенной на рис. 2.1, выполненная в среде Simulink, представлена на рис. 2.3.

Между тепловыми и электрическими цепями есть ряд отличий:

1. Источник теплового потока (тепловые потери) может иметь несколько выходов, число которых равно числу направлений отвода тепла, в то время как источник электрического потока (источник тока) имеет лишь один вход и один выход.

2. В ветви с последовательно соединенными источниками тепла потоки на разных участках не равны, в то время как в электрической цепи при последовательном соединении любых элементов ток постоянен.

Рис. 2.3. Электрическая схема замещения тепловой цепи статора АД в среде Simulink

Правила построения электрической схемы на основе тепловой:

1. Тепловые сопротивления заменяются электрическими без какого-либо изменения топологии схемы.

2. На месте источника теплового потока в эквивалентной электрической цепи ставится узел, в который входит ветвь от эквивалентного источника тока. При этом свободный вывод источника тока заземляется.

Выясним, при каких условиях электрическая цепь, изображенная на рис. 2.3, подобна тепловой цепи, изображенной на рис. 2.1. Для этого воспользуемся первой теоремой подобия. Для определения условий, критериев и масштабов подобия выполним определенные действия в следующем порядке:

1. Определим соответствие величин оригинала и модели:

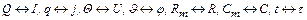, (2.36)

где j – плотность тока, А/м².

При этом тепловое сопротивление вычисляется по-разному для разных участков тепловой цепи. Это приводит к разному соответствию величин. Для участков с заданной теплопроводностью

, (2.37)

для участков с заданной теплоотдачей

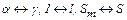. (2.38)

2. Введем масштабы подобия:

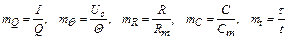. (2.39)

3. Приведем уравнения тепловых и электрических процессов к безразмерному виду

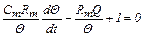. (2.40)

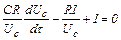. (2.41)

4. Подставим во второе уравнение величины из первого уравнения с соответствующими масштабными коэффициентами:

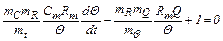. (2.42)

5. Уравнение (2.40) тождественно уравнению (2.42) при выполнении следующих условий:

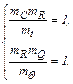(2.43)

6. Пять величин оригинала, входящие в уравнение (2.40), имеют следующие размерности:

. (2.45)

Анализ размерностей показывает, что все пять размерностей могут быть построены из трех независимых размерностей. Значит, три масштаба могут быть независимыми, а два являются зависимыми. В качестве зависимых удобнее всего выбрать масштабы 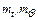. Остальным масштабам m_C, m_R и m_Q можно присвоить любые произвольные значения. В целях упрощения модели величины сопротивлений и емкостей в схеме на рис. 2.3 можно выбрать равными соответствующим величинам тепловых сопротивлений и теплоемкостей, то есть m_C = m_R = m_Q = 1.

Зависимые масштабы должны быть рассчитаны из (2.43):

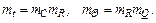(2.46)

Дата добавления: 2014-10-23