Теоретическая часть. Лабораторная работа № 1. Исследование электрической схемы замещения механического амортизатора

Лабораторная работа № 1. Исследование электрической схемы замещения механического амортизатора

ЦЕЛЬ РАБОТЫ: ознакомиться с методом математического моделирования с использованием электрических схем замещения на примере механического колебательного узла.

Механическая схема амортизатора представлена на рис. 1.1,а. Узел содержит пружину с коэффициентом жесткости k и масляный демпфер с коэффициентом трения r. Масса всей системы равна m. На систему действует внешняя сила F. Электрическая схема замещения амортизатора изображена на рис. 1.1,б.

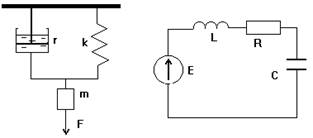
а) б)

Рис. 1.1. Механическая схема амортизатора (а) и его схема замещения (б)

В данной задаче амортизатор (механическая цепь) является оригиналом, электрическая цепь – моделью. Механическая цепь на рис. 1.1,а описывается уравнением

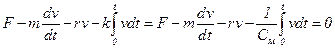, (1.1)

где F – внешняя сила, Н; m – масса механического узла, кг; v – скорость, м/с; t – время, с; r – коэффициент сопротивления демпфера, Н^.с/м; k – коэффициент упругости пружины, Н/м; С_м – механическая емкость пружины, м/Н.

Электрическая цепь на рис. 1.1,б описывается уравнением

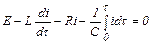, (1.2)

где E – ЭДС, В; L – индуктивность, Гн; i – сила тока, А; τ – время, с; R – электрическое сопротивление, Ом; С – электрическая емкость, Ф.

Оба уравнения являются изоморфными, что позволяет применить к ним первую теорему подобия. То есть при определенных условиях электрическая цепь рис. 1.1,б может являться моделью механической цепи рис. 1.1,а. Для определения условий, критериев и масштабов подобия выполним определенные действия в следующем порядке:

1. Определим соответствие величин оригинала и модели:

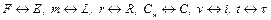. (1.3)

2. Введем масштабы подобия:

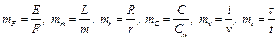. (1.4)

3. Приведем оба уравнения к безразмерному виду:

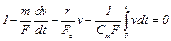. (1.5)

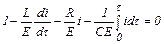. (1.6)

4. Подставим во второе уравнение величины из первого уравнения с соответствующими масштабными коэффициентами:

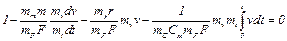. (1.7)

Получим

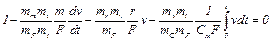. (1.8)

5. Уравнение (1.8) тождественно уравнению (1.5) при выполнении следующих условий:

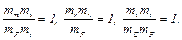(1.9)

6. Подставив вместо масштабов выражения (1.4), получим выражения для трех критериев подобия

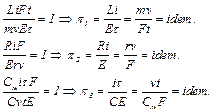(1.10)

7. Если разделить все слагаемые уравнений (1.1)-(1.2) не на первое слагаемое, а на второе, то получим еще три критерия

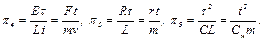(1.11)

При делении на третье слагаемое получим

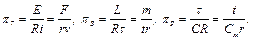(1.12)

При делении на четвертое слагаемое получим

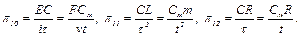(1.13)

8. Анализ двенадцати критериев позволяет выявить повторяющиеся критерии и оставить всего шесть критериев: π₁, π₂, π₃, π₅, π₆ и π₉. Три из этих критериев являются независимыми, а три остальные – зависимыми. То есть дополнительные три критерия подобия можно было получить также путем комбинации трех изначально полученных критериев:

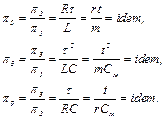(1.14)

9. Проведем анализ размерностей величин, входящих в уравнение оригинала (1.1):

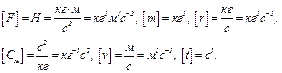(1.15)

Анализ размерностей показывает, что размерности всех шести величин могут быть построены из трех основных размерностей системы СИ: кг, м, с. Это значит, что из шести масштабов подобия три масштаба являются независимыми, то есть их значения можно выбрать произвольным образом.

В качестве независимых удобнее всего выбрать масштабы 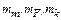. То есть при моделировании механической цепи электрической схемой замещения величины сопротивления, индуктивности и емкости можно выбрать произвольным образом.

Остальные три масштаба оказываются зависимыми, то есть их значения должны быть получены на основе независимых масштабов решением системы уравнений (1.9):

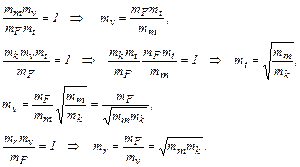(1.16)

Задаваясь произвольными значениями сопротивления, индуктивности и емкости, для заданных параметров механической цепи рассчитываем независимые масштабы 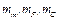. Затем из (1.16) рассчитываются зависимые масштабы 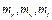и сопротивление 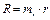. Из этих элементов строится электрическая цепь, процессы в которой i=f(τ) фиксируются осциллографом и с помощью масштабов подобия пересчитываются в зависимость v=f(t). Использование возможностей Simulink по совмещению электрической цепи со структурной схемой позволяет получить зависимость x=f(t) путем интегрирования сигнала v=f(t).

Дата добавления: 2014-10-23