Сложная и обратная функции

Способы задания функции

ФУНКЦИЯ ОДНОЙ ПЕРЕМЕННОЙ, ОСНОВНЫЕ ПОНЯТИЯ

МАТЕМАТИЧЕСКИЙ АНАЛИЗ (1 СЕМЕСТР)

1. Определение. Пусть даны два множества X и Y. Если каждому элементу x из множества X по некоторому правилу f соответствует единственный элемент y из множества Y, то говорят, что на множестве X определена функция y = f (x) с областью определения X = D(f) и областью изменения Y = E(f).

При этом x считают независимой переменной, или аргументом функции, а y – зависимой переменной или функцией.

Частным значением функции y = f (x) при фиксированном значении аргумента x = x₀ называют y₀ = f (x₀).

Графиком функции y = f (x) называют геометрическое место точек M(x;f (x)), где x Î D(f) и f (x) Î E(f).

1) Аналитический способ – способ задания функции с помощью формулы.

Различают несколько способов аналитического задания функции:

а) Функция задана явно формулой y = f (x).

Например: 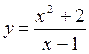, где D(y)=(-∞;1)(1;+∞).

б) Функция задана неявно уравнением, связывающем x и y: F (x; y) = 0.

Например: 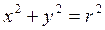- уравнение окружности с центром в начале координат и радиусом r. Если выразить из этого уравнения y через x, то получится две функции:

и ,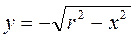

которые имеют область определения 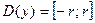, а области значений этих функций будут: для первой - , для второй - .

в) Функция задана параметрически с помощью некоторого параметра t, причем и аргумент x, и функция y зависят от этого параметра:

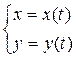
Например: можно задать окружность 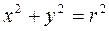с помощью параметрических уравнений:

2) Табличный способ задания функции.

Например, таблицы Брадиса задают функции y = sin x, y = cos x и другие.

3) Графический способ задания функции, когда зависимость функции от её аргумента задается графически.

Определение 1. Пусть функция y = f (U) определена на множестве D(f), а функция U = g (x) определена на D(g), причем E(g)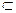D(f).

Тогда функция y = F (x) = f (g (x)) называется сложной функцией (или функцией от функции или суперпозицией функций f и g).

Определение 2. Пусть задана функция y = f (x) взаимно однозначно отображающая множество X= D(f) на множество Y= E(f).

Тогда функция x = g (y) называется обратной к функции y = f (x).

То есть любому y E(f) соответствует единственное значение x D(f), при котором верно равенство y = f (x).

Замечание. Графики функций y = f (x) и x = g (y) представляют одну и ту же кривую. Если же у обратной функции независимую переменную обозначить x, а зависимую через y, то графики функций y = f (x) и y = g (x), будут симметричны относительно биссектрисы первого и третьего координатных углов.

Дата добавления: 2014-10-15