
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгоритм вычисления пределов
|
|
|
|
Замечательные пределы.
Теорема. Первый замечательный предел имеет вид 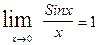 .
.
Так как под переменной х обычно понимают «что угодно», то из первого замечательного предела следует его применение в более общих ситуациях. Главное, чтобы та величина, которая стремится к нулю, была записана под знаком синуса и в знаменателе отношения. Так, например,
 и
и 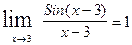 и
и
 . Присмотритесь к изменению аргумента х и изменению величины, записанной под знаком синуса и в знаменателе.
. Присмотритесь к изменению аргумента х и изменению величины, записанной под знаком синуса и в знаменателе.
Второй замечательный предел. Теорема. 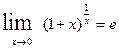 .
.
е – число Непера, упоминавшееся в обзоре основных элементарных функций.
Этот предел может иметь вид  .
.
Обозначим символически все возможные случаи, которые встречаются при вычислении пределов так  ;
;  ;
;  ; 0
; 0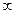 ; 1
; 1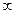 ; 0о;
; 0о; 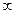 о. Все символы кроме первого обозначают в математике так называемую неопределенность. Это значит, что предельное значение установить затруднительно. Для развязки возникшей неприятности применяют специальные приемы, о которых речь ниже.
о. Все символы кроме первого обозначают в математике так называемую неопределенность. Это значит, что предельное значение установить затруднительно. Для развязки возникшей неприятности применяют специальные приемы, о которых речь ниже.
1-й шаг алгоритма всегда один и тот же. «Подставим» предельное значение аргумента под знак предела и определим тип предела.
2-й шаг. Зависит от полученного типа предела. И потому здесь несколько разных действий.
2.1.Если тип предела  и В
и В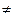 0, А
0, А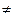
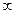 , В
, В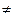
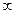 , то тип предела и даст сам предел.
, то тип предела и даст сам предел.
2.2. Если тип предела  и В=0, то рассматривают дробь, у которой знаменатель уменьшается, а числитель ограничен и потому дробь растет неограниченно. Мы получаем бесконечный предел (см. частные случаи пределов).
и В=0, то рассматривают дробь, у которой знаменатель уменьшается, а числитель ограничен и потому дробь растет неограниченно. Мы получаем бесконечный предел (см. частные случаи пределов).
2.3.Если А=0 и В=0, то имеем предел типа  - неопределенность. Здесь могут быть разные случаи.
- неопределенность. Здесь могут быть разные случаи.
2.3.1.Если под знаком предела есть синусы, косинусы, тангенсы или обратные им функции, то следует преобразовать выражение под знаком предела так, чтобы можно было применить 1-й замечательный предел. Он тоже имеет такой тип.
2.3.2.Если под знаком предела записано отношение полиномов, то их следует разложить на множители, используя значение корней. Затем до перехода к пределу сократить на множитель, вносящий неопределенность. И далее вернуться к п.1. алгоритма.
2.3.3.Если под знаком предела имеется иррациональность, то перенести ее из числителя в знаменатель (и-или наоборот). Затем обработать полученное по п.2.3.2. и вернуться к п.1.
2.4.Если тип предела  , то преобразуют дробь, используя связь бмв и ббв(см. частные случаи пределов), и переходят к п.2.3.
, то преобразуют дробь, используя связь бмв и ббв(см. частные случаи пределов), и переходят к п.2.3.
2.5.Если тип предела 0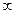 , то преобразуют произведение в дробь, используя связь бмв и ббв, и переходят к пунктам 2.3 или 2.4. соответственно.
, то преобразуют произведение в дробь, используя связь бмв и ббв, и переходят к пунктам 2.3 или 2.4. соответственно.
2.6.Если тип предела 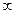 -
-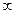 , то поступают в зависимости от выражений, дающих ббв.
, то поступают в зависимости от выражений, дающих ббв.
2.6.1.Если эти выражения – рациональные дроби, то иногда достаточно привести их к общему знаменателю и перейти к п.2.3.
2.6.2. Если эти выражения – разность иррациональностей, то следует перенести ее из числителя в знаменатель и вернуться после упрощения к п.1.
2.7. Пределы типа 1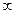 обрабатывают в направлении применения 2-го замечательного предела (сначала выписывают нужную в работе 1; затем оставшиеся слагаемые в основании преобразуют; затем в показателе записывают величину, обратную преобразованному выражению и старый показатель; затем новый показатель умножают на величину так, чтобы сохранилось общее равенство; затем применяют замечательный предел и обрабатывают оставшийся показатель). См. примеры.
обрабатывают в направлении применения 2-го замечательного предела (сначала выписывают нужную в работе 1; затем оставшиеся слагаемые в основании преобразуют; затем в показателе записывают величину, обратную преобразованному выражению и старый показатель; затем новый показатель умножают на величину так, чтобы сохранилось общее равенство; затем применяют замечательный предел и обрабатывают оставшийся показатель). См. примеры.
2.8. Пределы типа 0о; 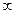 о обрабатывают по одной схеме на основании основного логарифмического тождества. Пусть мы имеем предел вида
о обрабатывают по одной схеме на основании основного логарифмического тождества. Пусть мы имеем предел вида  .
.
Тогда выражение под знаком предела следует записать так
 =
=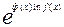 и затем вычислять предел показателя полученного выражения. Во всех случаях там получаются пределы, рассмотренные ранее.
и затем вычислять предел показателя полученного выражения. Во всех случаях там получаются пределы, рассмотренные ранее.
Пример 3.5. Вычислить пределы.
1. 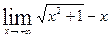 .
.
Решение. Это тип предела 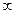 -
-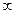 ; он содержит иррациональности и потому переносим иррациональность в знаменатель, умножив числитель и знаменатель но сопряженное числителю
; он содержит иррациональности и потому переносим иррациональность в знаменатель, умножив числитель и знаменатель но сопряженное числителю 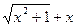 . Получаем
. Получаем 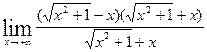 =
=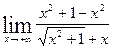 =
= . Получен предел типа
. Получен предел типа  , в которой знаменатель растет, а числитель неизменен. По п.2.2. ответом будет 0.
, в которой знаменатель растет, а числитель неизменен. По п.2.2. ответом будет 0.
2.  .
.
Решение. Имеем тип предела 1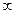 .Обрабатываем его в направлении 2-го замечательного. Получаем последовательно
.Обрабатываем его в направлении 2-го замечательного. Получаем последовательно
 =
=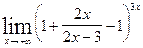 =
=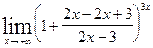 = (сохранена 1 и сделано приведение к общему знаменателю. Предстоит упростить)
= (сохранена 1 и сделано приведение к общему знаменателю. Предстоит упростить)
= =
= = (т.к.
= (т.к. 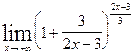 =е)
=е)
= =
=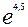 (т.к.
(т.к. 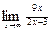 =
= по схеме 2.3.2)
по схеме 2.3.2)
6.4.Примеры эквивалентных бмв.
При достаточно малых х (т.е. х близких к 0) эквивалентными будут:
Sinx и х; tgx и x; arcSinx и x; arctgx и x; ex и 1+x; ln(1+x) и x; 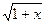 и 0,5x;
и 0,5x;
 и
и 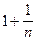 x. Эти сведения удобны в приближенных вычислениях и вычислении пределов.
x. Эти сведения удобны в приближенных вычислениях и вычислении пределов.
Контрольные вопросы и задания для самостоятельной подготовки:
1. Числовые последовательности.
2. Операции над числовыми последовательностями.
3. Ограниченные и неограниченные последовательности.
4. Бесконечно большие и бесконечно малые последовательности.
5. Понятие сходящейся последовательности.
6. Основные свойства сходящихся последовательностей.
7. Предельный переход в неравенствах.
8. Определение и признак сходимости монотонных последовательностей.
9. Число е.
10. Предел функции в точке.
11. Односторонние пределы.
12. Предел функции при 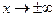
13. Теоремы о пределах функций, связанные арифметическими действиями.
14. Два замечательных предела.
15. Бесконечно большие и бесконечно малые функции.
16. Определение непрерывности функции. Арифметические действия над непрерывными функциями.
17. Определение и классификация точек разрыва функции.
18. Теорема об устойчивости знака непрерывной функции.
19. Прохождение непрерывной функции через любое промежуточное значение.
20. Ограниченность непрерывной функции на отрезке.
21. Теорема о достижении функцией, непрерывной на отрезке, своих точных граней.
22. Понятие равномерной непрерывности функции.
23. Вычислить 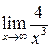
24. Вычислить 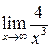
25. Вычислить 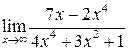
26. Вычислить 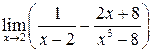
27. Вычислить 
28. Вычислить 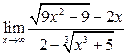
29. Вычислить 
30. Вычислить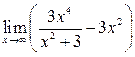
31. Вычислить
32. Вычислить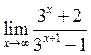
33. Вычислить
34. Вычислить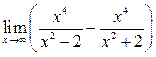
35. Вычислить 
36. Вычислить 
37. Вычислить 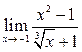
38. Вычислить 
39. Вычислить 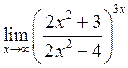
40. Вычислить 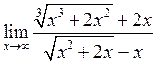
41. Вычислить 
42. Вычислить 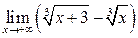
43. Вычислить 
44. Вычислить 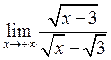
45. Вычислить 
46. Вычислить 
47. Вычислить 
48. Вычислить 
49. Вычислить 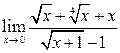
50. Вычислить 
51. Вычислить 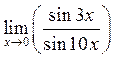
52. Вычислить 
53. Вычислить 
54. Вычислить 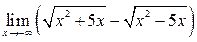
55. Вычислить 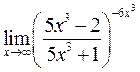
56. Вычислить 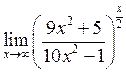
57. Вычислить 
58. Вычислить 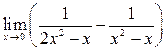
59. Вычислить 
60. Вычислить 
61. Вычислить 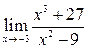
62. Вычислить 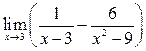
63. Вычислить 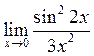
|
|
|
|
|
Дата добавления: 2014-10-23; Просмотров: 3214; Нарушение авторских прав?; Мы поможем в написании вашей работы!