Цилиндры и поверхности вращения

Из поверхностей, отличных от 2-го порядка рассмотрим два частных случая.

Пусть задано уравнение F(x;y)=0 в пространстве. И требуется установить, как выглядит поверхность.

Комментарий. Т.к. сказано, что уравнение задано в пространстве, то отсутствие в уравнении некоторых переменных не противоречит определению поверхности в пункте 6.1.

Рассуждаем так. Добавим к этому уравнению уравнение z=0. Тогда

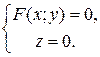
Эта система есть линия на плоскости хОу. На ней можно взять точку М(х;у). Если теперь эту точку перемещать вдоль Oz, не меняя х и у этой точки, то уравнение поверхности F(x;y)=0 будет тождественно выполняться, т.к. тождественно выполняется первое уравнение системы. Значит поверхность образована движением прямой, параллельной Oz и пересекающей данную линию на плоскости. Естественно эту поверхность назвать цилиндрической. У нее две характеристики, определяющие ее вид: кривая F(x;y)=0 при z=0 – направляющая цилиндра; и прямая, пересекающая эту кривую, перпендикулярная плоскости расположения кривой и называемая образующей цилиндра.

Вывод: всякое уравнение с двумя переменными в пространстве определяет цилиндрическую поверхность с образующей, параллельной отсутствующей координате и направляющей – кривой в плоскости переменных, записанных в уравнении поверхности.

Пусть дана плоская линия для определенности в плоскости хОу уравнениями

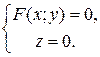
На ней можно взять точку М(х;у). Если теперь эту точку вращать около оси Oх, то точка опишет окружность с центром на оси Ох и радиусом, равным у точки М. Уравнение этой окружности Z2+Y2=y2. В уравнении большими буквами записаны фактически меняющиеся координаты точки на окружности, а малое у – это радиус. Такие же окружности описывают все точки кривой и образуется поверхность вращения. На каждой окружности этой поверхности х=Х. Если из уравнения окружности выразить у и подставить в уравнение кривой, то получим F(Х,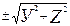)=0. Но последнее уравнение содержит три переменные и потому является уравнением поверхности вращения взятой в начале линии относительно Ох.

Вывод: если в некотором уравнении квадраты двух переменных имеют одинаковые коэффициенты, то это поверхность вращения. А механизм получения уравнения поверхности, образованной вращением некоторой линии относительно координатной оси, представлен выше.

Контрольные вопросы и задания для самостоятельной подготовки:

1. Уравнение прямой на плоскости. Общее уравнение.

2. Уравнение прямой на плоскости. Уравнение линии в отрезках.

3. Уравнение прямой на плоскости. Уравнение с угловым коэффициентом.

4. Линии второго порядка. Эллипс.

5. Линии второго порядка. Парабола.

6. Линии второго порядка. Гипербола.

7. Прямая и плоскость в пространстве.

8. Даны три вектора: 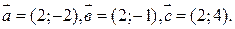Составить Уравнение прямой, проходящей через точку А (5;-1) под углом 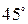к оси Ох.

9. Составить уравнение плоскости, проходящей через точку М (1;-2;3) и перпендикулярной вектору ;

10. Составить уравнение плоскости, проходящей через точку М (1;-2;3) и параллельно плоскости 3х-4у+5z+6=0;

11. Составить уравнение плоскости, проходящей через точку М (1;-2;3) и точку 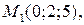и параллельной оси Оу;

12. Составить уравнение плоскости, проходящей через точку М (1;-2;3) и проходящей через ось Оz.

13. Составить уравнение плоскости, проходящей через прямую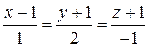и точку М (2;0;1)

14. Составить уравнение плоскости, проходящей через две параллельные прямые

15. В треугольнике АВС даны уравнения: стороны АВ , высоты ВМ , высоты АМ , где точка М – точка пересечения высот. Найти уравнения сторон АС, ВС и стороны СМ.

16. Две стороны параллелограмма заданы уравнениями и 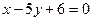. Диагонали его пересекаются в начале координат. Найти уравнения сторон параллелограмма и его диагоналей.

17. Ординаты все точек окружности сокращены втрое. Написать уравнение полученной новой кривой.

18. Эллипс, симметричный относительно осей координат, проходит через точки и . Найти полуоси, координаты фокусов и эксцентриситет эллипса.

19. Для гиперболы 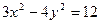найти действительную и мнимую полуоси; координаты фокусов; эксцентриситет; уравнения асимптот.

20. Составить уравнения параболы, проходящей через точки и симметрично относительно оси Ох.

РАЗДЕЛ 2. МАТЕМАТИЧЕСКИЙ АНАЛИЗ И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.

Дата добавления: 2014-10-23