Уравнения 2-й степени в пространстве

Определение. Уравнением второго порядка в пространстве (уравнением поверхности 2-го порядка) называют уравнение вида

a₁₁x²+a₂₂y²+a₃₃z²+2a₁₂xy+2a₁₃xz+2a₂₃yz+a₄₁x+a₄₂y+a₄₃z+ a₄₄=0 (7.1)

Мы познакомимся только с уравнением (6.3), в котором отсутствуют произведения текущих координат. В этом случае имеется возможность выделить полные квадраты по переменным и получить уравнение поверхности в каноническом виде. Последние и будем изучать более подробно.

Для исследования канонических уравнений поверхностей второго порядка используют метод сечений. В самом простом виде он выглядит так: проводят серии плоскостей, параллельных координатным плоскостям и по результатам (виду сечений) делают вывод о форме поверхности. Эта работа похожа на работу томографа при исследовании внутренних органов человека в медлабораториях или работу топографа при топографической съемке местности.

Реализуем метод при построении поверхности 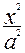++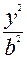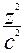=1

Рассечем поверхность плоскостями z=h. Тогда в сечении получим

,

Из этой системы видно, что h не может превышать z=hс. Что означает – поверхность расположена между двумя плоскостями – выше h=-c и ниже h=c. Более того, в сечениях получаются эллипсы, самый большой из которых расположен в плоскости z=0. Чем дальше от плоскости хОу, тем меньше эллипс. И на высоте с эллипс вырождается в точку.

Если провести аналогичные серии плоскостей. параллельных другим координатным плоскостям, то получим похожие выводы. Следовательно, поверхность образована скольжением эллипсов по эллипса и называется трехосным эллипсоидом.

Дата добавления: 2014-10-23