
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Производная и дифференциал
|
|
|
|
Таблица и основные правила.
Применяя алгоритм, легко получить такие правила поиска производных:
(с)’=0; x’=1; (u(x) 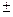 v(x))’=(u(x))’
v(x))’=(u(x))’ 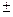 (v(x))’.
(v(x))’.
Сложнее получить формулу (u(x)v(x))’=u’(x)v(x)+u(x)v(x). Получим ее, несколько сократив запись алгоритма. Получаем f(x)= u(x)v(x). Тогда f(x+ )= u(x+
)= u(x+ )v(x+
)v(x+ ). Но лучше это записать так f(x+
). Но лучше это записать так f(x+ )= (u(x)+
)= (u(x)+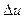 )(v(x)+
)(v(x)+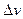 ), потому что при изменении переменной х изменяются и переменные u и v. Далее получаем f(x+
), потому что при изменении переменной х изменяются и переменные u и v. Далее получаем f(x+ )- f(x)== (u(x)+
)- f(x)== (u(x)+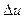 )(v(x)+
)(v(x)+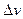 )--u(x)v(x)= v(x)
)--u(x)v(x)= v(x) 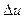 +u(x)
+u(x) 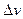 . Разделим полученное на
. Разделим полученное на  и вычислим предел отношения. Получим рабочую формулу.
и вычислим предел отношения. Получим рабочую формулу.
По аналогичной схеме можно получить производную частного 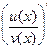 =
=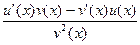 . Для доказательства достаточно записать f(x+
. Для доказательства достаточно записать f(x+ )=
)= в виде f(x+
в виде f(x+ )=
)= и далее продолжить алгоритм вычисления производной
и далее продолжить алгоритм вычисления производной 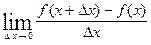 =
= =
=
 =
= =
=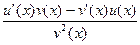 .
.
Если y=f(x) и х=ф(у) взаимно обратные функции, то их производные связаны соотношением y’x=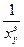 . Доказательство следует из
. Доказательство следует из 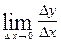 =
=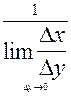
Если y=f(x) и х=ф(t) (т.е. y=f(ф(t)) – сложная функция), то y’t= y’xx’t, где y’x= f’x(x), а x’t = ф’t(t).
Доказательство следует из цепочки преобразований  =
=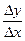
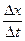 и затем вычислить предел полученного при
и затем вычислить предел полученного при 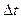
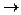 0, что приведет к тому что
0, что приведет к тому что 
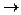 0.
0.
Бывают ситуации, когда функция y=f(x) задана параметрически, т.е. в виде 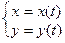 . Тогда используют тот факт, что отношение
. Тогда используют тот факт, что отношение 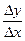 всегда можно преобразовать по схеме
всегда можно преобразовать по схеме 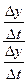 . А при вычислении производной получить в ответе запись y’=
. А при вычислении производной получить в ответе запись y’= .
.
Используя эти правила, получаем сначала таблицу производных основных элементарных функций.
 |
Функция Ее производная Вывод формулы и комментарии

y=ax, a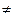 1,a>0; y’= ax lna; Имеем y+
1,a>0; y’= ax lna; Имеем y+ = ax+
= ax+ ,
,  =ax+
=ax+ -ax = ax (a
-ax = ax (a -1)
-1)
Теперь  =
=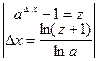 =
=
= ax  = ax lna.
= ax lna.
y=ex, y’= ex; Как частный случай для предыдущей
формулы.
y=lnx y’=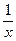 ; Т.к. х=eу, то на основании связи производных
; Т.к. х=eу, то на основании связи производных
взаимно обратных функций имеем
(lnx)’x=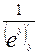 ==
== =
=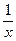 .
.
y=х, y’=х, Имеем y=х = elnx. Далее используем
предыдущую формулу и производную от
сложной
функции y’= elnx 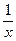 =х.
=х.
y=Sinx y’=Cosx Имеем  =Sin(x+
=Sin(x+ )-Sinx=2Cos
)-Sinx=2Cos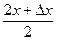 Sin
Sin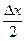 ;
;
теперь y’= 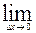
 =
=
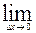
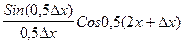 =Cosx.
=Cosx.
y=Cosx y’=-Sinx В самом деле (Cosx)’=(sin( -x))’=
-x))’=
Cos( -x)(-x)’=-Sinx. Применена формула
-x)(-x)’=-Sinx. Применена формула
Приведения и производная сложной
функции.
y=tgx y’= Достаточно записать производную от дроби
Достаточно записать производную от дроби
(tgx)’= далее преобразовать рез-т.
далее преобразовать рез-т.
y=arcSinx y’=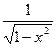 В самом деле, по условию x=Siny. Для
В самом деле, по условию x=Siny. Для
взаимно обратных функций имеем (arcSinx)’=
=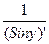 =
= =
=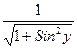 =
=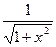 .
.
y=arctgx y’= Схему получения смотри выше.
Схему получения смотри выше.
y=arcCosx y’=-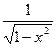 Ввиду того, что arcCosx=
Ввиду того, что arcCosx= -arcSinx.
-arcSinx.
y=arcctgx y’=- Схему получения смотри выше.
Схему получения смотри выше.
В тех случаях, когда применить вышеприведенные правила и таблицу затруднительно, можно использовать прием, называемый логарифмическим дифференцированием. Пусть мы имеем y=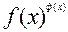 . Тогда невозможно применить ни одну их записанных выше формул. Поступают так. Сначала логарифмируем обе части равенства и получаем lny=ф(х)ln(f(x)). Теперь возьмем производную от каждой части равенства, зная, что у – это функция от х. Получаем
. Тогда невозможно применить ни одну их записанных выше формул. Поступают так. Сначала логарифмируем обе части равенства и получаем lny=ф(х)ln(f(x)). Теперь возьмем производную от каждой части равенства, зная, что у – это функция от х. Получаем 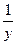 y’=ф’(x)lnf(x)+ф(x)
y’=ф’(x)lnf(x)+ф(x)  f’(x). Из полученного равенства найдем требуемое
f’(x). Из полученного равенства найдем требуемое
y’=y(ф’(x)ln(f(x))+ф(x)  f’(x))=
f’(x))=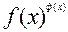 (ф’(x)ln(f(x))+ф(x)
(ф’(x)ln(f(x))+ф(x)  f’(x)).
f’(x)).
Возможен и другой подход. Имеем y=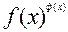 =
=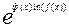 . После чего можно искать производную по правилу сложной функции. Получаем
. После чего можно искать производную по правилу сложной функции. Получаем
y’=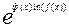 (ф’(x)lnf(x)+ф(x)
(ф’(x)lnf(x)+ф(x)  f’(x))=
f’(x))= 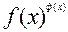 (ф’(x)ln(f(x))+ф(x)
(ф’(x)ln(f(x))+ф(x)  f’(x)).
f’(x)).
Если же функция y=f(x) задана неявно, т.е. уравнением F(x;y)=0, то для поиска производной следует взять производную от равенства F(x;y)=0, зная, что у= f(x), хотя f(x) и неизвестна. Затем из полученного равенства находят y’.
Из связи предела и бмв для производной получаем  =f’(x)
=f’(x) +
+ , где - бмв. Т.к. слагаемые в сумме, записанной справа неравноценны по величине (произведение
, где - бмв. Т.к. слагаемые в сумме, записанной справа неравноценны по величине (произведение  имеет порядок малости более высокий, чем
имеет порядок малости более высокий, чем  , а первое слагаемое имеет порядок малости, такой же как и
, а первое слагаемое имеет порядок малости, такой же как и  ), то одно из них выделим в виде определения.
), то одно из них выделим в виде определения.
Опр. Главная, линейная относительно  часть приращения функции называется дифференциалом функции и обозначается dy.
часть приращения функции называется дифференциалом функции и обозначается dy.
Получаем dy= f’(x) . Иногда используют обозначение df(x)= f’(x)
. Иногда используют обозначение df(x)= f’(x) .
.
Т.к.  =dx, то обозначение дифференциала принимает симметричный вид
=dx, то обозначение дифференциала принимает симметричный вид
dy= f’(x)dx или df(x)= f’(x)dx или dy=y’dx.
Используя новое понятие, можно сказать что производная есть отношение дифференциалов функции и аргумента. Этот факт дает новые формы записи для символа производной: y’=f’(x)=y’(x)= 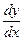 =
= =
= =
= .
.
Можно достаточно просто истолковать дифференциал – это приращение касательной к кривой в данной точке. (cм. Рис 4.1. DB – это приращение  функции y=f(x); DC – приращение dy касательной плоскости. Простейшие свойства дифференциала вытекают из соответствующих свойств производной (аддитивности, однородности и линейности)
функции y=f(x); DC – приращение dy касательной плоскости. Простейшие свойства дифференциала вытекают из соответствующих свойств производной (аддитивности, однородности и линейности)
С помощью дифференциала можно получить известную формулу для вычисления производной параметрически заданной функции. Имеем 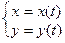 . Тогда отношение y’=
. Тогда отношение y’=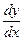 принимает вид y’=
принимает вид y’=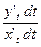 и затем получить y’=
и затем получить y’= .
.
Используем дифференциал для приближенных вычислений ввиду того, что  , которое мы не знаем во многих случаях, можно приближенно заменить на величину dy, которое всегда можно вычислить. Это положено в основу приближенной формулы f(x+
, которое мы не знаем во многих случаях, можно приближенно заменить на величину dy, которое всегда можно вычислить. Это положено в основу приближенной формулы f(x+ )=f(x)+
)=f(x)+  =f(x)+f’(x)
=f(x)+f’(x)  . Пусть нам требуется вычислить значение функции у= f(x), но точно сделать это затруднительно. Тогда можно предложить алгоритм применения дифференциала:
. Пусть нам требуется вычислить значение функции у= f(x), но точно сделать это затруднительно. Тогда можно предложить алгоритм применения дифференциала:
-выбери точку хо достаточно близко к точке х и вычисли значение f(xо);
-вычисли значение f’(xо) и значение  =х- хо;
=х- хо;
-вычисли приближенно f(x), заменив  на f’(xо)
на f’(xо)  .
.
Пример 4.1. Вычислите приближенно ln1,2. Решение. Выбираем подходящую по записи функцию f(x)=lnx. Нам предстоит вычислить ее значение при х=1,2. Сделать это мы не можем. Выберем хо=1. Найдем
dy= f’(xо)  при
при  =1,2-1=0,2. Получаем (lnx)'=
=1,2-1=0,2. Получаем (lnx)'=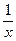 =1 при хо=1. Теперь вычислим приближенное значение ln1,2=ln1+1*0,2=0,2. О погрешности результата в данный момент речи не идет – нужно хотя бы приближенное значение.
=1 при хо=1. Теперь вычислим приближенное значение ln1,2=ln1+1*0,2=0,2. О погрешности результата в данный момент речи не идет – нужно хотя бы приближенное значение.
Дифференциал обладает свойством инвариантности (неизменность формы записи в зависимости от вида задания функции).
Пусть у= f(x) и х=ф(t). Тогда dy=f’tdt. Но dx=ф’tdt. C другой стороны мы знаем, что f’t=f’хф’t. Поэтому dy=f’tdt= f’хф’tdt=f’х dx – т.е. форма записи сохранилась.
|
|
|
|
|
Дата добавления: 2014-10-23; Просмотров: 450; Нарушение авторских прав?; Мы поможем в написании вашей работы!