Первообразная. Неопределенный интеграл и его свойства

Тема 9. Неопределенный интеграл.

Определение. F(x) называют первообразной f(x) (для f(x)) на [a;b], если для любого х из этого отрезка F(x) дифференцируема и F’(x)=f(x). Так F(x)=x² будет первообразной для f(x)=2x для всех действительных чисел.

Теорема. Если F₁(x) и F₂(x) первообразные f(x) на [a;b], то любого х из этого отрезка имеет место равенство F₁(x) - F₂(x) =С.

Следствие. Если F(x) одна из первообразных для f(x) то любая Ф(х)=F(x)+C – тоже первообразная.

Так Ф(x)=2x +С будет первообразной f(x)=x² для всех действительных чисел.

Определение. Множество первообразных для данной f(x) на [a;b] называют неопределенным интегралом и обозначают .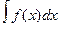

Из определения следует справедливость тождества 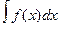= F(x)+C.

Термины и обозначения: f(x) - подынтегральная функция; f(x)dx – подынтегральное выражение; х (записанный в символе dx) - аргумент (переменная) интегрирования; - символ интегрирования.

Все рассмотренное – процесс, обратный поиску производной.

Следствия.

1.Производная от НИ равна подынтегральной функции ’=f(x).

2.Дифференциал от НИ равен подынтегральному выражению d =f(x)dx.

3. Неопределенный интеграл от производной равен подынтегральной функции с точностью до постоянного слагаемого С. F’(x)dx= F(x)+C.

4. Неопределенный интеграл от дифференциала равен выражению под знаком дифференциала точностью до постоянного слагаемого С. dF(x)= F(x)+C.

Все это разные вариации определения.

Свойства.

1.Константу - множитель можно выносить из-под знача НИ. 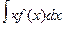= кF(x)+C.

2.НИ от суммы функций равен сумме интегралов от слагаемых. =+.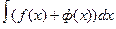

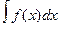3.Независимость от аргумента. 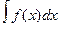=== 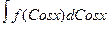F(x)= F(u)= F(Cosx).

Так Cosx d(Cosx)=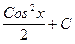, (lnx+1) d(lnx+1)=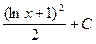 как и для хdx =.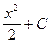

9. 2. Таблица основных неопределенных интегралов

1.1. 1.	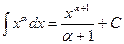1.2. 6.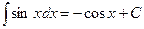
1.3. 2.	1.4. 7.
1.5. 3.	1.6. 8.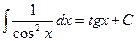
1.7. 4.	1.8. 9.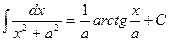
1.9. 5.	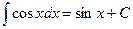1.10. 10.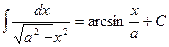

В отличие от производных, где каждой ситуации предписано правило ее обработки, при поиске интегралов вся теория заканчивается на этой таблице. Фактически для поиска интеграла остаются только определение и следствия из него, свойства и таблица. А это значит, что все остальное следует преобразовывать эвристическими приемами (или по уже готовым рекомендациям, но не правилам!) к таблице и определению. В качестве контроля ответа может служить только обратный процесс – от результата возьми производную. И, если результат равен подынтегральной функции, то имеется некоторая степень уверенности в правильности выполнения интегрирования.

Дата добавления: 2014-10-23