
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Рациональные дроби
|
|
|
|
Определение. Рациональной дробью называют выражение 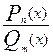 . Где
. Где  и
и 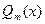 – полиномы от переменной х.
– полиномы от переменной х.
Определение. Простейшими дробями 1-4-го типов называют выражения, соответственно, вида: 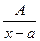 ;
; 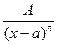 ;
; 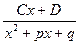 ;
; 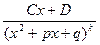 , где квадратные трехчлены в знаменателях не имеют действительных корней.
, где квадратные трехчлены в знаменателях не имеют действительных корней.
Интегралы от простейших дробей находят по таким схемам.
I-й тип. Вынесем за знак интеграла константу А и подведем под знак дифференциала знаменатель. Получим 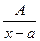 dx=А
dx=А
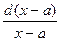 =Aln(x-a)+C.
=Aln(x-a)+C.
II-й тип обработаем аналогично I-му. Но используем интеграл от степени.
III-й тип. Обрабатываем в несколько приемов.
1-й. Сначала найдем производную от знаменателя 2x+p.
2-й шаг. Если в числителе С не нуль, то преобразуем числитель к виду суммы производной от знаменателя и константы Cx+D=  (2x+p)+D-
(2x+p)+D-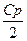 .
.
3-й шаг. Разобьем исходный интеграл на сумму двух интегралов, числитель первого – производная 2х+р; числитель второго – константа

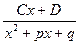 dx==
dx==

 dx+ (D-
dx+ (D-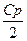 )
)
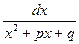 .
.
4-й шаг. После подведения числителя 1-го слагаемого под знак интеграла первое слагаемое дает табличный интеграл от логарифма знаменателя. Во втором слагаемом в знаменателе выдели полный квадрат в трехчлене и тогда второе слагаемое даст arctg(…). Получаем 
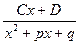 dx =
dx = ln(x2+px+q)+
ln(x2+px+q)+
(D-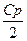 )
)
 =
= ln(x2+px+q)+ (D-
ln(x2+px+q)+ (D-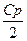 )
) 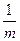 arctg
arctg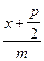 +K.
+K.
Комментарий. Рекомендуется не запоминать окончательный ответ (хотя и не возбраняется), а пройти на паре примеров весь алгоритм. Этого будет достаточно для усвоения процесса. Этот процесс встречается очень часто в других разделах математики и других дисциплин (ТОЭ, механика, сопромат).
IV-й тип обрабатывается по схеме типа III. Только в конце всегда получается типовой интеграл, который обрабатывают по рекуррентной формуле

 =
=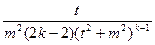 +
+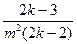

 (7.1)
(7.1)
Эту формулу можно получить такими приемами: 
 =
=
=

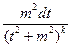 =
=

 =
= (
(
 -
- 
 ).
).
Первый интеграл сохранить, т.к. в нем степень знаменателя понижена. Во втором интеграле применить формулу интегрирования по частям, выбрав u=t остальное dv. И тогда степень знаменателя понизится. Затем привести подобные по интегралам с одинаковыми знаменателями степени k-1.
Пример. Найдите интеграл  . Решение. Подынтегральное выражение – простейшая дробь 4-го типа, т.к. трехчлен не имеет действительных корней. Производная от трехчлена равна 2х+2. Преобразованный числитель имеет вид
. Решение. Подынтегральное выражение – простейшая дробь 4-го типа, т.к. трехчлен не имеет действительных корней. Производная от трехчлена равна 2х+2. Преобразованный числитель имеет вид
0,5(2х+2)–2, а подынтегральная дробь приводит на с интегралам 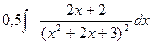 -
- . Далее первый интеграл дает после подведения под знак дифференциала 2х+2 0,5
. Далее первый интеграл дает после подведения под знак дифференциала 2х+2 0,5
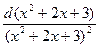 и по формуле для степенной функции получаем
и по формуле для степенной функции получаем  . Во втором интеграле в знаменателе выделим полный квадрат и преобразуем аргумент интегрирования – подведем под знак дифференциала константу 1. Получим
. Во втором интеграле в знаменателе выделим полный квадрат и преобразуем аргумент интегрирования – подведем под знак дифференциала константу 1. Получим 
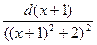 . Далее работаем по рекуррентной формуле (7.1) при к=2 и t=x+1 и m=
. Далее работаем по рекуррентной формуле (7.1) при к=2 и t=x+1 и m= . Получаем
. Получаем

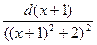 =
= +
+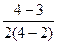

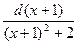 =
=
= +
+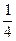
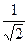 arctg
arctg . Если учесть первый интеграл и коэффициент –2 перед вторым интегралом, то получаем
. Если учесть первый интеграл и коэффициент –2 перед вторым интегралом, то получаем 
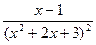 dx=
dx=
= -
-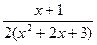 -
- arctg
arctg +С =-
+С =-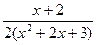 -
- arctg
arctg +С.
+С.
Теперь строим алгоритм интегрирования рациональной дроби.
1-й шаг. Проверяем, будет ли 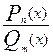 правильной (будет ли m>n)? Если будет, то переходим к шагу 3. Иначе выполняем шаг 2.
правильной (будет ли m>n)? Если будет, то переходим к шагу 3. Иначе выполняем шаг 2.
2-й шаг. Делим числитель на знаменатель ‘уголком’. Представляем неправильную дробь в виде суммы целой части и правильной дроби 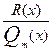 . От целой части берем интеграл как о суммы степеней. Для отыскания интеграла от правильной дроби выполняем шаг 3.
. От целой части берем интеграл как о суммы степеней. Для отыскания интеграла от правильной дроби выполняем шаг 3.
3-й шаг. Находим корни полинома Qm(x) и разлагаем его на множители
Qm(x)=(x-a)k1(x-b)k2…(x-c)k3(x2+p1x+q1)k4+(x2+p2x+q2)k5+…+(x2+p3x+q3)k6. При этом k1+k2 +… +k3 +2k4 +2k5 +…2k6 =m, а числа этом k1, k2,…, k3, k4 , k5, …,k6 - кратности корней.
4-й шаг. Записываем правильную дробь 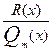 в виде суммы правильных простейших дробей
в виде суммы правильных простейших дробей
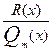 =
=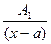 +
+ +…
+…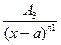 +…
+… +
+ +…
+… +…
+…
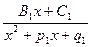 +
+  +…+
+…+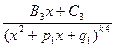 +…. Количество дробей должно быть равно количеству множителей в разложении с учетом кратности.
+…. Количество дробей должно быть равно количеству множителей в разложении с учетом кратности.
5-й шаг. Приводим сумму дробей справа к общему знаменателю. Т.к. между дробями стоит знак равенства и знаменатели равны, то приравниваем числители. Поучаем равенство двух полиномов одинаковой степени. Такие полиномы равны, если: равны коэффициенты при одинаковых степенях х; подставить в обе части равенства одинаковые значения аргумента.
6-й шаг. Приравниваем коэффициенты при одинаковых степенях х в полиномах справа и слева и(или) подставляем в обе части некоторые значения аргументов (если корни действительные и простые, и если корни комплексные и простые). Получаем линейную систему с неизвестными коэффициентами. Решаем систему и получаем конкретные простейшие дроби.
7-й шаг. Интегрируем сумму простейших дробей и вместе с результатом шага 2 получаем ответ.
|
|
|
|
|
Дата добавления: 2014-10-23; Просмотров: 443; Нарушение авторских прав?; Мы поможем в написании вашей работы!