Методы интегрирования

Пусть х=ф(t) –монотонная и непрерывная на некотором промежутке функция. Если на соответствующем промежутке изменения переменной х функция f(x) интегрируема, то справедливо равенство =.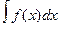

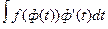Записанное равенство называют формулой замены в неопределенном интеграле. Применяют ее тогда, когда правая часть оказывается ближе к табличному интегралу (см. Комментарий выше).

Док. В самом деле, т.к. F(x) - первообразная для f(x), то F(ф(t)) – будет первообразной для f(ф(t))ф’(t). И потому F’(ф(t))= F’_ф(ф(t))ф’_t(t)= f(ф(t))ф’(t). Откуда следует f(ф(t))ф’(t)dt= F(ф(t))+C= F(x)+C= .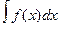

Комментарий. Имеются два подхода использования формулы замены. Один из них изложен выше. В другом (более употребимом) случае заменяют не переменную х на некоторое выражение, а выражение, связывающее х, заменяют одной переменной. А далее – как обычно.

Пример.

Найти = .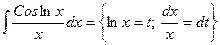

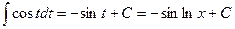Иногда замену переменных используют в еще одном виде – подведении под знак дифференциала, используя простое соотношение dx=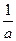d(ax+b) для любых а 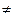0 и в. По знак дифференциала подводят такую группу, чтобы интеграл сменил аргумент интегрирования (см. следствия из определения) и при этом принял табличный вид.

Пример 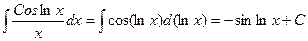– результат совпадает с предыдущим примером.

Пусть каждая из функций u(x) и v(x) дифференцируемы на некотором промежутке и существует первообразная для произведения u’(x)v(x). Тогда на этом промежутке существует первообразная для u(x)v’(x) и справедливо равенство

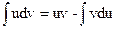, называемое формулой интегрирования по частям.

Рекомендации по применению этой формулы.

Возможно одного шага применения формулы недостаточно. Тогда ее применяют кратно.

Возможно применение формулы приведет к сохранению подынтегрального выражения. Не следует тревожиться по такому случаю, т.к. это даже хорошо.

Выбор частей u и v основан на опыте. Только решение конкретных примеров обеспечит навыком выбора частей.

Пример. Вычислить интеграл

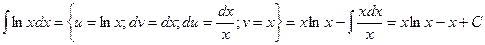
Некоторые классы интегрируемых функций.

Т.к. в практических приложениях предстоит интегрировать выражения разной сложности, то следует научиться отличать, то что приводит к конкретному ответу от того, что ни при каких условиях не приведет к результату. Умению отличать одно от другого и приемам интегрирования посвящен данный раздел.

Рассмотрим некоторые классы функций, для которых опытным путем разработаны приемы отыскания неопределенных интегралов. Фактически приемы эти приводят к таблице основных интегралов. Отметим также, что в интегральном исчислении принята такая схема работы – если новый, ранее неизвестный интеграл преобразован к уже известному классу, задача считается решенной.

Дата добавления: 2014-10-23