Основные понятия. Тема 12 Функции нескольких переменных

Тема 12 Функции нескольких переменных

Все понятия, справедливы для функций 2-х переменных, остаются верными и для функций любого конечного числа переменных.

Определение. Если паре (х;у) из множества М по закону f ставится в соответствие единственное действительное z, то говорят, что на М задана функция двух переменных и обозначают этот факт z=f(x;y).

Множество М называют областью определения функции.

Аналогично определяется функция любого иного числа переменных.

Т.к. геометрически паре (х;у) соответствует точка на координатной плоскости хОу, а величине z соответствует аппликата в трехмерном пространстве, то геометрически факт z=f(x;y) можно истолковать как поверхность в пространстве.

Гораздо труднее дать интерпретацию функции 3-х переменных. Поэтому введем понятие поля: если в каждой точке M некоторого пространства задано значение величины U, то говорят, что в пространстве задано поле U и обозначают этот факт U=U(M).

Т.к. точка М может зависеть от нескольких координат и еще менять свое местоположение от времени, то можно провести простую классификацию полей. Если М меняет свое положение в зависимости от времени t, то поле называют нестационарным, в противном случае – стационарным. Кажется парадоксальным, но поле скоростей точек при течении воды в трубопроводе при открытом кране – стационарное поле!

Если М(х), то поле одномерно (осевое); если М(х,у) – поле плоское; если М(х,у,z) – поле пространственное.

Если U скалярная величина, то поле скалярное; если U вектор. То и поле векторное.

Определение. Окрестность точки (х,у) – круг некоторого радиуса и с центром в точке. Для пространственной точки окрестность – это шар.

Определение. -окрестность точки - это круг радиуса 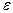и с центром в этой точке.

Определение. Точка Р – внутренняя для некоторого множества, если любая -окрестность ее содержит только точки этого множества.

Определение. Точка Р граничная для множества, если любая -окрестность ее содержит как точки множества, так и точки, ему не принадлежащие.

Определение. Множество граничных точек – граница.

Определение. Областью называют множество открытое и связное. Открытость – множество состоит только из внутренних точек. Связность – любые две точки множества можно соединить непрерывной линией, состоящей только из внутренних точек.

Если множеству принадлежат его внутренние точки и точки границы – это замкнутая область.

Если множество целиком принадлежит кругу конечного радиуса с центром в начале координат, то это ограниченное множество.

Определение. Линией уровня функции z=f(x;y) называют множество точек области определения, в каждой из которых выполняется равенство С= f(x;y).

Для функции 3-х переменных справедливо понятие поверхности уровня.

Дата добавления: 2014-10-23