
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Частные производные и дифференциалы
|
|
|
|
Пусть дана z=f(x;y). Дадим переменной х приращение 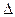 х. Тогда функция z=f(x;y) получит некоторое приращение только за счет приращения х. Обозначим его значком
х. Тогда функция z=f(x;y) получит некоторое приращение только за счет приращения х. Обозначим его значком 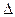 хz и назовем частным приращением.
хz и назовем частным приращением.
Определение. Частной производной от функции по данному аргументу называют предел отношения частного приращения функции к вызвавшему его приращению аргумента, если последнее стремится к нулю.
Символически это факт записывают по разному: z’x; f’x; 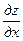 ;
; 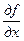 ;
; 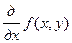 и т.д. Обратите внимание – в третьей и четвертой записях не записано отношение, а записан один символ! Читается всегда так ”частная производная от … по …”. Неверно читать “ дэ от … по дэ…”.
и т.д. Обратите внимание – в третьей и четвертой записях не записано отношение, а записан один символ! Читается всегда так ”частная производная от … по …”. Неверно читать “ дэ от … по дэ…”.
Распространим на частую производную известный геометрический ее смысл – частная производная характеризуют скорость изменения функции в направлении выбранной координатной оси.
Теорема(необходимое условие существования ЧП). Если f(x;y) имеет ЧП в данной точке, то функция непрерывна в этой точке.
Определение. Главная часть частного приращения функции, линейная относительно частного приращения аргумента называется частным дифференциалом функции и обозначается dxz= f’x х или dxz= f’x dх.
х или dxz= f’x dх.
Пусть дана f(x;y). При переходе от точки М к точке Мо эта функция получит приращение 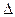 z, которое в отличие от частного следует называть полным приращением функции.
z, которое в отличие от частного следует называть полным приращением функции.
Определение. Если  z удается представить в виде А
z удается представить в виде А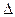 х+В
х+В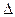 у+
у+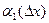
 х+
х+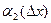
 у, то говорят, что z=f(x;y) дифференцируема, а выражение А
у, то говорят, что z=f(x;y) дифференцируема, а выражение А х+В
х+В у называют полным дифференциалом и обозначают dz.
у называют полным дифференциалом и обозначают dz.
Выведем формулу для вычисления полного дифференциала. Имеем  z= =f(x+
z= =f(x+ х;y+
х;y+ у)- f(x;y)= f(x+
у)- f(x;y)= f(x+ х;y+
х;y+ у) - f(x;y+
у) - f(x;y+ у) + f(x;y+
у) + f(x;y+ у) - f(x;y)= f(x+
у) - f(x;y)= f(x+ х;y+
х;y+ у)- f(x;y+
у)- f(x;y+ у) +(f(x;y+
у) +(f(x;y+ у)- f(x;y)). Для каждой разности применим формулу Лагранжа конечных отношений и получим
у)- f(x;y)). Для каждой разности применим формулу Лагранжа конечных отношений и получим 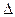 z= f’x(C1;y+
z= f’x(C1;y+ у)
у) х+ f’y(x;C2)
х+ f’y(x;C2) у, где точки C1 и C2 расположены на участках приращения переменных. Но, т.к.
у, где точки C1 и C2 расположены на участках приращения переменных. Но, т.к. 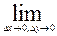 f’x(C1;y+
f’x(C1;y+ у)= f’x(х;y) и
у)= f’x(х;y) и  f’y(x;C2) = f’у(х;y), то из связи пределов с бесконечно малыми получаем
f’y(x;C2) = f’у(х;y), то из связи пределов с бесконечно малыми получаем
 z= f’x(х;y)
z= f’x(х;y)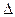 х+ f’у(х;y)
х+ f’у(х;y) у+
у+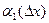
 х+
х+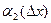
 у
у
Отсюда видно, что dz = А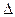 х+В
х+В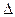 у= f’x(х;y)
у= f’x(х;y)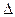 х+ f’у(х;y)
х+ f’у(х;y)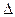 у= f’x(х;y)dх+ f’у(х;y)d у. Т.е. полный дифференциал равен сумме частных дифференциалов.
у= f’x(х;y)dх+ f’у(х;y)d у. Т.е. полный дифференциал равен сумме частных дифференциалов.
Полный дифференциал удобно применять в вычислениях.
Пример. Вычислите приближенно 1,01 2,03. Решение. Подберем подходящую по виду функцию z=xy. Возьмем точку Мо достаточно близкую к точке М (1,01; 2,03) и такую, чтобы легко можно было вычислить значение функции в этой точке. Такой будет Мо (1;2). Тогда z(Мо)=1. При переходе от точки Мо к точке М функция получит некоторое приращение 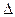 z, которое мы не знаем. Но можем вычислить приближенно, заменив полным дифференциалом dz(Mo). Получаем
z, которое мы не знаем. Но можем вычислить приближенно, заменив полным дифференциалом dz(Mo). Получаем  z=dz= f’x(х;y)
z=dz= f’x(х;y) х+ f’у(х;y)
х+ f’у(х;y) у. Найдем частные производные функции в точке Мо. f’x(Мо) = y xy-1 =1. f’y(Мо) =xylnx=0.
у. Найдем частные производные функции в точке Мо. f’x(Мо) = y xy-1 =1. f’y(Мо) =xylnx=0.
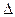 х=1,01-1=0,01;
х=1,01-1=0,01;  у=2,03-2=0,03. Получаем
у=2,03-2=0,03. Получаем  z=1(0,01)+0(0,03)=0,01. Окончательно 1,01 2,03 =1+0,01=1,01.
z=1(0,01)+0(0,03)=0,01. Окончательно 1,01 2,03 =1+0,01=1,01.
|
|
|
|
|
Дата добавления: 2014-10-23; Просмотров: 404; Нарушение авторских прав?; Мы поможем в написании вашей работы!