Электронная плотность

Пространственное распределение заряда электрона называется электронной плотностью. Исходя из того, что вероятность нахождения электрона в элементарном объеме d V равна |ψ|²d V, можно рассчитать функцию радиального распределения электронной плотности.

Если за элементарный объем принять объем шарового слоя толщиной d r на расстоянии r от ядра атома, то

d V = 4π r ²d r,

а функция радиального распределения вероятности нахождения электрона в атоме (вероятности электронной плотности), равна

W_r = 4π r ²|ψ|²d r

Она представляет собой вероятность обнаружения электрона в сферическом слое толщиной d r на определенном расстоянии слоя от ядра атома.

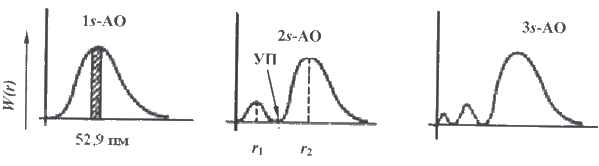
рисунок 9

Для 1 s -орбитали вероятность обнаружения электрона максимальна в слое, находящемся на расстоянии 52,9 нм от ядра. По мере удаления от ядра атома вероятность обнаружения электрона приближается к нулю. В случае 2 s -орбитали на кривой появляются два максимума и узловая точка, где вероятность обнаружения электрона равна нулю. В общем случае для орбитали, характеризующейся квантовыми числами n и l, число узлов на графике функции радиального распределения вероятности равно (n − l − 1).

Точное решение уравнения Шредингера удается найти лишь в редких случаях, например, для атома водорода и гипотетических одноэлектронных ионов, таких как He⁺, Li²⁺, Be³⁺. Атом следующего за водородом элемента - гелия - состоит из ядра и двух электронов, каждый из которых притягивается к обоим ядрам и отталкивается от другого электрона. Уже в этом случае волновое уравнение не имеет точного решения.

Поэтому большое значение имеют различные приближенные методы. С помощью таких методов удалось установить электронное строение атомов всех известных элементов. Эти расчеты показывают, что орбитали в многоэлектронных атомах не сильно отличаются от орбиталей атома водорода (эти орбитали называют водородоподобными). Главное отличие - некоторая сжатость орбиталей из-за большего заряда ядра. Кроме того, для многоэлектронных атомов найдено, что для каждого энергетического уровня (при данном значении главного квантового числа n) происходит расщепление на подуровни. Энергия электрона зависит уже не только от n, но и от орбитального квантового числа l. Она увеличивается в ряду s -, p -, d -, f -орбиталей (рис. 10).

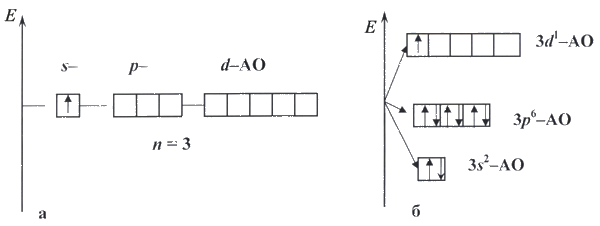
рисунок 10

Для высоких энергетических уровней различия в энергиях подуровней достаточно велики, так что один уровень может проникать в другой, например

6 s < 5 d 4 f < 6 p.

Заселение атомных орбиталей для многоэлектронного атома в основном (то есть энергетически наиболее выгодном) состоянии происходит в соответствии с определенными правилами.

Дата добавления: 2014-10-23