Тема 1. Комплексные числа

Понятие числа

Основные понятия и термины: понятие комплексного числа, геометрическое изображение комплексного числа, алгебраическая форма комплексного числа, д ействие над комплексными числами в алгебраической форме.

Краткое изложение теоретических вопросов:

Первоначально «число» характеризовало количество предметов в каком-либо их наборе и служило для счета. Эти числа назвали натуральными числами: 1, 2, 3, …. Эти числа можно складывать и умножать. Но вот вычитать и делить натуральные числа можно не всегда, например, 3-5 или 3:8.

Стремление сделать операции вычитания и деления всегда выполнимыми привело к появлению отрицательных и дробных чисел, тем самым расширив понятие «число» до понятий «целых» и «рациональных» чисел.

После того как в Древней Греции была доказана иррациональность числа 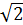, т.е. невозможность решить уравнение x ² = 2, имея в своем распоряжении только рациональные числа, человечество вновь столкнулось с необходимостью расширить свой числовой запас.

Так появилось множество действительных (или вещественных) чисел как множество всех рациональных и иррациональных чисел.

В дальнейшем стремление сделать выполнимой операцию извлечения корня из любого действительного (в том числе и отрицательного) числа, привело к понятию комплексного числа вида: z = a + b ×i, где i = - «мнимая единица» - корень квадратного уравнения: x ² + 1 = 0.

Известный советский детский писатель С. Маршак с шуточным ужасом писал о школьнике, у которого в задаче: «… и вышло у меня в ответе два землекопа и две трети»

Можно представить себе, как бы он ужаснулся ответу: «2 + 3×i», увидев мнимых землекопов.

Введение комплексных чисел позволило выполнять любые действия с ними. Оказалось также, что на множестве комплексных чисел любое алгебраическое уравнение имеет решение! Это утверждение называется основной теоремой алгебры.

Особенно плодотворным оказалось применение комплексных чисел в задачах, возникающих в естествознании: теории электромагнитного поля, теории электрических цепей, гидро- и аэромеханике (учении о движении жидкостей и газов), квантовой механике, теории механических колебаний и др.

Когда-то великий К.Ф. Гаусс сказал: «Математика – это царица наук». Но эти примеры показывают, что математика занимает в мире совсем иное место, куда более почетное, она – служанка многих наук, она доставляет им тот необходимый аппарат, с помощью которого последние могут описывать процессы, факты и явления. Недаром Ландау называл математику «сверхъестественной наукой».

Построим на комплексной плоскости следующие комплексные числа:
, ,
, ,
, , ,

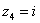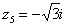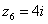
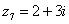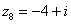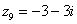Комплексными числами называются числа вида z=a+bi, где a и b–

действительные числа, а число i, определяемое равенством i²=-1, называется мнимой единицей.

Два комплексных числа z₁=a₁+b₁i и z₂=a+b₂i называются равными, если a₁= a₂ и b₁= b₂

Запись комплексного числа в виде z=a+bi называется алгебраической формой записи комплексного числа. Действительное число a называется действительной частью комплексного числа z=a+bi, а bi – его мнимой частью.

Два комплексных числа называются взаимно сопряженными (обозначаются z и ), если их действительные части равны, а мнимые отличаются знаками.

Комплексные числа вида a+bi и - a – bi называются противоположными.

Множество комплексных чисел обозначается буквой С.

- Напомню, что комплексным числом называется выражение вида z=a+bi, где a и b – действительные числа, i²=-1

ВОПРОСЫ:

- Как называется число а и как называется число b? (действительная и мнимая части комплексного числа)

- Как изображается комплексное число на плоскости? (точкой или радиус-вектором)

- Верно ли, что одной и той же точкой на плоскости могут изображаться 2 различных комплексных числа? (нет)

- Как называется расстояние от точки, изображающей комплексное число до начала координат? (модуль)

- Чему равен модуль комплексного числа? (квадратному корню из суммы квадратов действительной и мнимой части)

- Раскройте смысл понятия «аргумент комплексного числа» (угол между положительным направлением оси абсцисс и радиус-вектором точки- Чему равен тангенс аргумента? (отношению мнимой части комплексного числа к его действительной части)

- Верно ли, что любое действительное число является комплексным? Почему? (да; 5 = 5 + 0i)

- Верно ли, что любое комплексное число является действительным? (нет)

Дата добавления: 2014-10-23