Уравнение баланса энергии

ЛЕКЦИЯ №8

Закон об изменении энергии или переноса энергии для некоторого объема формулируется следующим образом.

Изменение во времени полной энергии некоторой массы вещества равно сумме мощностей внешних объемных и поверхностных сил, приложенных к рассматриваемой массе и ее поверхности, сложенной с отнесенным к единице времени количеством тепла, которое протекает вследствие теплопроводности через поверхность, ограничивающую выделенную массу. Приведенный закон можно записать в виде

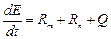, (8.1)

где 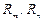- мощности массовых и поверхностных сил, приложенных к рассматриваемой массе и ее поверхности;

Q - количество тепла, протекающее в единицу времени через поверхность рассматриваемого объема.

Полная энергия единицы объема Е есть сумма внутренней и кинетической энергии, т.е.

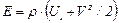. (8.2)

Внутренняя энергия единицы массы при условии, что газ совершенен, равна произведению абсолютной температуры Т на удельную теплоемкость при постоянном объеме 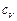, т.е.

. (8.3)

Следовательно, полная энергия единицы объема равна

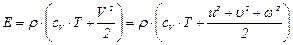. (8.4)

Работа массовых или объемных сил может быть вычислена как сумма работ составляющих массовых сил, отнесенных к единице массы, X, У и Z на перемещениях 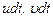и 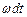. Следовательно, мощность массовых сил, отнесенных к единице объема, равна

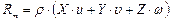. (8.5)

К каждой грани элементарного параллелепипеда приложены силы с нормальными и касательными составляющими. Рассмотрим работу сил, приложенных к граням, перпендикулярным к оси х. Работа нормальной составляющей 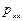, приложенной к грани 1, лежащей в координатной плоскости уz, равна

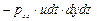, (8.6)

а работа нормальной составляющей, приложенной к грани 2, удаленной от координатной плоскости уz на расстояние dx, будет

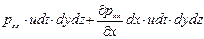. (8.7)

Очевидно, сумма мощностей нормальных составляющих сил, приложенных к граням, перпендикулярным к оси х, отнесенная к единице объема, будет равна .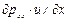

Соответствующая сумма мощностей касательных составляющих, приложенных к тем же граням, запишется

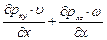. (8.8)

Аналогичные расчеты мощностей поверхностных сил, приложенных к площадкам, нормальным к осям у и z, дают

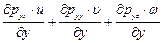; (8.9)

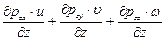. (8.10)

Таким образом, мощность поверхностных сил единицы объема будет

(8.11)

Количество входящего и выходящего из данного объема тепла Q

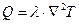. (8.12)

Тогда, подставив в уравнение (8.1) выражения для Е, 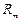, 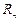и Q по формулам (8.4), (8.5), (8.11) и (8.12), окончательно получим уравнение баланса энергии

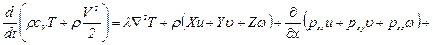
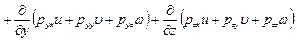. (8.13)

Мощность массовых сил можно представить в виде скалярного произведения

. (8.14)

Аналогичным образом представим мощность поверхностных сил в виде

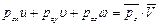, (8.15)

где 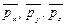- векторы напряжений поверхностных сил, приложенных к граням, перпендикулярным осям х, y и z. Тогда уравнение баланса энергии может быть представлено в виде

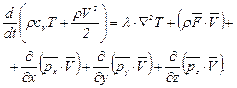(8.16)

Для жидкой и газовой среды уравнение энергии может быть также представлено в интегральной форме

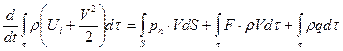, (8.17)

где 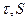- элементарный объем и его контрольная поверхность;

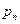- напряжение поверхностных сил;

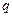- количество теплоты, подводимое к единице массы за единицу времени.

Дата добавления: 2014-10-31