Турбулентное течение

Для турбулентного течения характерно перемешивание жидкости, пульсации скоростей и давлений.

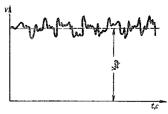
Рис. 8.1. Пульсация скорости в турбулентном потоке

Скорость беспорядочно колеблется около некоторого осреднённого v_оср по времени значения, которое в данном случае остается постоянным. Турбулентное течение всегда является неустановившимся, так как значения скоростей и давлений, а также траектория частиц, изменяются по времени.

Распределение скоростей при турбулентном течении более равномерное, а нарастание скорости у стенки более крутое, чем при ламинарном течении.

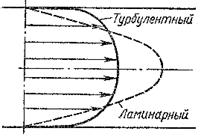
Рис. 8.2. Профили скоростей в ламинарном

и турбулентном потоках

Так как при турбулентном течении отсутствует слоистость потока и происходит перемешивание жидкости, закон трения Ньютона в этом случае выражает лишь малую часть полного касательного напряжения.

Благодаря перемешиванию жидкости и непрерывному переносу количества движения в поперечном направлении касательное напряжение τ₀ на стенке трубы в турбулентном потоке значительно больше, чем в ламинарном. В связи с этим потери энергии при турбулентном течении жидкости в трубах также получаются иными, нежели при ламинарном.

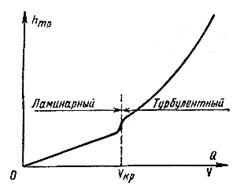
Рис. 8.3. Зависимость 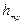от v и Q

Ввиду сложности турбулентного течения и трудностей его аналитического исследования до настоящего времени для него не имеется достаточно строгой и точной теории.

Турбулентное движение в практических расчетах описывают не мгновенными, а осредненными во времени скоростями

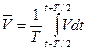, (8.18)

где Т – интервал усреднения.

Разность 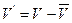называют пульсационной скоростью.

Для оценки пульсационных составляющих (добавок) скорости вводят стандарт, равный среднеквадратичному отклонению пульсационных добавок

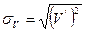. (8.19)

Степенью (интенсивностью) турбулентности 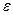называют отношение среднеквадратичного отклонения пульсационной составляющей (добавки) скорости к характерной скорости потока (к осредненной местной скорости в данной точке, к средней по вертикали, к средней по живому сечению, к максимальной скорости). Обычно за характерную скорость принимают среднюю скорость потока, осредненную местную скорость в данной точке или динамическую скорость

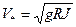, (8.20)

где R – гидравлический радиус;

J – гидравлический уклон.

Исследования показывают, что наиболее общие результаты для описания пульсирующих скоростей при турбулентном движении получаются, если в качестве масштаба скоростей принять динамическую скорость 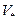, т.е.

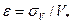. (8.21)

В качестве примера рассмотрим поток жидкости в прямолинейной цилиндрической трубе круглого сечения (осесимметричный поток). Структуру потока в трубе при турбулентном режиме движения обычно представляют в виде приближенной двухслойной схемы (модели). На твердой стенке скорости, в том числе и пульсационные, равны нулю. Вблизи твердой стенки находится очень тонкий слой, в котором преимущественное влияние имеют касательные напряжения, рассчитываемые по закону вязкого трения Ньютона. Поэтому рассматриваемый слой называют вязким подслоем потока.

В пределах вязкого подслоя скорость линейно увеличивается от нуля на стенке до некоторого значения на границе слоя. Раньше считали, что в пределах этого тонкого слоя движение полностью ламинарное, пульсации скорости, давления, касательного напряжения в нем отсутствуют и поэтому его называли ламинарным подслоем (пленкой).

Остальную часть поперечного сечения трубы считают занятой турбулентным ядром потока, где и происходят интенсивные пульсации скорости и перемешивание частиц жидкости.

Уравнения движения, выраженные через осредненные скорости для случая турбулентного неустановившегося движения несжимаемой жидкости носят название уравнений Рейнольдса и имеют вид

В проекции на ось х:

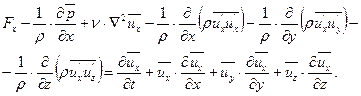(8.22)

Величины типа 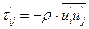, входящие в уравнение Рейнольдса, называются турбулентными напряжениями. Связь между ними и скоростями деформаций устанавливается на основе гипотез, составляющих основу полуэмпирических теорий турбулентности (гипотеза М. Буссинеска, гипотеза Л. Прандтля, гипотеза Дж. Тейлора, гипотеза Т. Кармана и др.). В большинстве случаев для практических расчетов, связанных с турбулентным течением жидкостей в трубах, пользуются экспериментальными данными, систематизированными на основе теории гидродинамического подобия.

Основной расчетной формулой для потерь напора при турбулентном течении в круглых трубах является эмпирическая формула, называемая формулой Дарси - Вейсбаха и имеющая следующий вид:

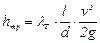. (8.23)

Эта основная формула применима как при турбулентном, так и при ламинарном течении; различие заключается лишь в значениях коэффициента .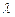

Дата добавления: 2014-10-31