И потока реальной (вязкой) жидкости

Уравнение Д. Бернулли для струйки

Одномерные потоки жидкостей и газов

ЛЕКЦИЯ №10

Одномерным называют движение, при котором скорость, давление, плотность, температура и другие параметры зависят лишь от одной координаты, направление которой совпадает с направлением вектора скорости. Если параметры одномерного движения не зависят от времени, движение является стационарным, если зависят – нестационарным.

В действительности одномерного движения не существует, однако введение его понятия и выяснение его закономерностей позволяет упрощенно решать многие задачи практики. Таким представлением движения широко пользуются в гидравлике, поэтому гидравлику часто называют наукой об одномерном движении.

При одномерном движении потоки конечных размеров обычно рассматривают как совокупности элементарных струек, скользящих одна по другой без перемешивания.

Ранее при рассмотрении интеграла уравнения движения жидкости для различных случаев было получено уравнение Д. Бернулли для линии тока и, соответственно, элементарной струйки идеальной несжимаемой жидкости в виде

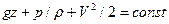. (10.1)

При переходе от элементарной струйки идеальной жидкости к потоку реальной (вязкой) жидкости, имеющему конечные размеры и ограниченному стенками, необходимо учесть неравномерность распределения скоростей по сечению, а также потери энергии (напора). То и другое является следствием вязкости жидкости.

При движении вязкой жидкости вдоль твердой стенки, например, в трубе, происходит торможение потока вследствие влияния вязкости, а также из-за действия сил молекулярного сцепления между жидкостью и стенкой. Поэтому наибольшего значения скорость достигает в центральной части потока, а по мере приближения к стенке она уменьшается практически до нуля. Получается распределение скоростей, подобное тому, которое показано на рис. 10.1.

Рис. 10.1. Распределение скоростей в реальном потоке

жидкости

Неравномерное распределение скоростей означает скольжение (сдвиг) одних слоев или частей жидкости по другим, вследствие чего возникают касательные напряжения (напряжения трения). Кроме того, движение вязкой жидкости часто сопровождается вращением частиц, вихреобразованием и перемешиванием. Все это требует затрат энергии, поэтому удельная энергия движущейся вязкой жидкости не остается постоянной, как в случае идеальной жидкости, а постепенно расходуется на преодоление сопротивлений и, следовательно, уменьшается вдоль потока. Из-за неравномерного распределения скоростей приходится вводить в рассмотрение среднюю по сечению скорость 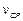, а также среднее значение удельной энергии жидкости в данном сечении.

Прежде чем приступить к рассмотрению уравнения Д. Бернулли для потока вязкой жидкости, сделаем следующее допущение: будем считать, что в пределах рассматриваемых поперечных сечений потока справедлив основной закон гидростатики: .

Здесь предполагается, что при движении жидкости отдельные струйки оказывают одна на другую в поперечном направлении такое же давление, как слои жидкости в неподвижном состоянии. Это соответствует действительности, когда течение в данных поперечных сечениях является параллельноструйным.

Введем понятие мощности потока. Мощностью потока в данном сечении будем называть полную энергию, которую проносит поток через это сечение в единицу времени.

Выразим элементарную мощность (мощность элементарной струйки) в виде произведения полной удельной энергии жидкости в данной точке на элементарный массовый расход:

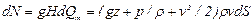. (10.2)

Мощность всего потока найдем как интеграл от предыдущего выражения по всей площади S:

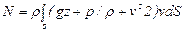, (10.3)

или, учитывая сделанное допущение,

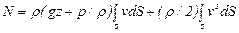. (10.4)

Найдем среднее по сечению значение полной удельной энергии жидкости делением полной мощности потока на массовый расход, т.е.

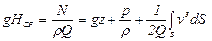. (10.5)

Умножив и разделив последний член уравнения на 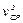, получим (переходя к напорам)

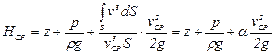, (10.6)

где a - безразмерный коэффициент Кориолиса, учитывающий неравномерность распределения скоростей и равный

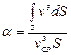. (10.7)

Коэффициент 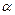представляет собой отношение действительной кинетической энергии потока в данном сечении к кинетической энергии того же потока и в том же сечении, но при равномерном распределении скоростей.

Возьмем два сечения реального потока, первое и второе, и обозначим средние значения полного напора жидкости в этих сечениях соответственно 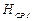и 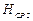. Тогда

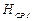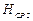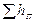=+, (10.8)

где 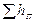- суммарная потеря полного напора на участке между рассматриваемыми сечениями. Используя формулу для , предыдущее уравнение можно переписать так:

. (10.9)

Это и есть уравнение Д. Бернулли для потока вязкой жидкости. От аналогичного уравнения для элементарной струйки идеальной жидкости полученное уравнение отличается членом, представляющим собой потерю полного напора, и коэффициентом, учитывающим неравномерность распределения скоростей. Кроме того, скорости, входящие в это уравнение, являются средними по сечениям.

Если для струйки идеальной жидкости уравнение Бернулли представляет собой закон сохранения механической энергии, то для потока реальной жидкости оно является уравнением баланса энергии с учетом потерь.

Уменьшение среднего значения полной удельной энергии жидкости вдоль потока, отнесенное к единице его длины, называется гидравлическим уклоном. Изменение удельной потенциальной энергии жидкости, отнесенное к единице длины, называется пьезометрическим уклоном. Очевидно, что в трубе постоянного диаметра с неизменным распределением скоростей указанные уклоны одинаковы.

Дата добавления: 2014-10-31